Rectangular Components:

Let a force F acting at O. Suppose a system of rectangular co-ordinates x, y and z along with 'O' as the origin. To find out the direction of the force, let us construct a parallelopiped (say, 'box') as illustrtaed in Figure.

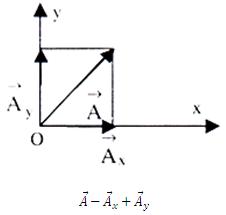
If θ_x, θ_y and θ_z are the angles made by F with respect to x, y and z axes respectively, then we obtain:

F_x = F cos θ _x,

F_y = F cos θ _y, and

F_z = F cos θ _z.

The angles θ_x, θ_y and θ_z define the direction of the force F (that acts in space) and cos θ_x, cos θ_y and cos θ_z are called as the direction cosines of the forces that are also (sometimes) represented respectively by l, m and n.

If i¯ , j¯ and k¯ are the unit vectors acting along with x, y and z axes as illustrated in Figure (b), then force F may be expressed in vector form as under :

F¯ = F¯x i¯ + F¯_y  j¯ + F¯_z  k¯ and the magnitude of F is given by following

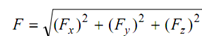
i.e.

F ² = (F_x) ² + (F_y) ² + (F_z )²

∴ 1 = (F_x /F ) +  ( F_y /F )+ ( F_z/F)

∴ l ²  + m²  + n²  = 1  ( Because   (F_x /F ) = l, ( F_y /F )  = m,  ( F_z/F)= n )

a well known result in 3-D geometry.