Bertrand Model of Duopoly:

Bertrand model of duopoly examines the price setting behavior of a firm by taking price as is the strategic variable.  The assumptions in it are the same as in Cournot model except that the firms have identical cost functions with constant marginal cost.  To arrive at the equilibrium, let us consider two firms A and B.

Given any price PB, set by firm B, firm A has 3 options:  
1) To set a price P_A > P_B                                                           
2) To set a price P_A = P_B  
3) To set a price P_A < P_B

In option 1, firm A looses the whole market. In 3, firm A captures the whole market and in 2, the market would be shared equally by them. Firm A will undercut B so long as MC_A  ≤ P_A .The same logic applies to firm B as well. This process will continue till P = MC_A = MC_B 

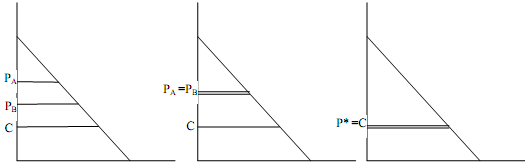
Diagrammatic Representation

In the following figures, we represent the process by which the firms reach equilibrium in the Bertrand model. The horizontal axis measures quantity of output produced by each firm along with cost (assumed to be identical). Along the vertical axis, we measure the price and marginal cost. In each of the figures, the horizontal line C represents the marginal cost (MC) of each firm.  When PA is greater than PB and both are greater than C as in Figure, firm A will be loosing the market to firm B as they are selling homogeneous product. Therefore, profit of firm A will be less than that of B and firm A will undercut firm B. In the next period firm B will be loosing the market to firm A and therefore, would undercut firm A. This process will go on until both charge the same price, as shown in Figure. In such a case, both of get an equal share of the market. However, it will not be an equilibrium situation because if any one of them reduces its price marginally, then it gets the full share of the market and earns more profit than when they were sharing the market equally. Finally, equilibrium will be attained when P_A = P_B = M_C. This is shown in Figure.

Figure gives a stable equilibrium because no one has any incentive to reduce or raise the price. If the former occurs, then there is the threat of loss because MC is greater than price. If the price is higher than the equilibrium price (P*), then there is a threat of potential loss of customers. Therefore, if price is greater than or less than P* it will have a tendency to move back to P*, which explains the stability of the equilibrium.

As in the Bertrand model P* = M_C, the solution is a competitive one and therefore output will be produced at the competitive level (unlike in the Cournot model where output produced by each duopolist was equal to one-third of the total market demand).