Back Propagation Or BP
The helpfulness of the network comes from its capability to respond to input patterns in any desirable fashion. For this to happen, it is essential to train the network to respond correctly to a specified input pattern. Training or knowledge acquisition happens by modifying the weights of the network to get the required output. The wieldiest used learning mechanism for multilayered perceptrons is the back propagation algorithm or BP.
The difficulty of finding best set of weights to minimize error in between the actual and expected response of the network can be considered a non-linear optimization problem. The BP algorithm uses illustration input-output pairs to train the network. An input pattern is represented to the network, and the network unit activations are determined on a forward pass through the network. The output unit activations present the network's current response to the specified input pattern. This output is then compared to a desired output for the specified input pattern, and, suppose a logistic activation function, error terms are determined for each output unit by the given operation as:
Δoi = dE/ dWij = (Ti - Aoi) Ahj(1 - Ahj)..............................Eqn (7)
Whereas:
- E is the network error
- Ti the desired activation of output unit i,
- Aoi the actual activation of output unit i,
- Ahj the actual activation of hidden unit j.
The weights leading into the hidden nodes are after that adjusted according to the given equation as:
ΔWij = - k Δoi Ahj................................Eqn(9)
Whereas k is the small constant often referred to the learning rate
The error terms are after that propagated back to the hidden layer, whereas they are used to determined the error terms for the units of the hidden layer as given below:
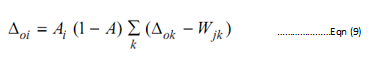
The weights from the input layer to the hidden layer are adjusted as in Eq. 8. Momentums terms may be added to the hidden layer are adjusted as in Eq. 8 to raise the rate of convergence. Such terms attempt to speed convergence by preventing search, from falling into shallow local minima, throughout search process. The strength of the error terms will depend upon the productivity of the current direction over a period of iterations and hence introduces a more global prospective to search. A wildly utilization of simple momentum strategy is given as:
- A momentum term was added to the weight update equation as given below:
ΔWij = (t + 1) = η∑ (Δjoj ) + α ΔWij (t )........................Eqn(10)
Whereas α is a momentum rate.
• If the total network error rise over a specific percentage, say 1%, from the previous iteration, the momentum rate α is instantly set to zero until the error is again decreased. This permits the search process to reorient itself it gets off track. One time the error is again decreased, the momentum rate is reset to its original value.
Throughout training, the total network error typically drops quickly during the initial iterations however easily become destabilized while using high learning rates. As the total network error converges towards zero, the rate of change in error gradually reduces, but the gradient descent search process such can tolerate higher learning rates before destabilizing. In order to acquire advantage of this technique, a small acceleration factor ω was utilized to accelerate the learning rate from a small initial value as 0.01 to some maximum value as 0.75 over some thousand iterations. The acceleration happens in a compound fashion, increasing the learning rate at all iteration according to the given equation:
η= ω η ........................Eqn (11)
It ensures that large increase in the learning rate does not happen until the convergence process has stabilized. Employ of the acceleration factor was highly effective, typically decreasing convergence time by thousands of iterations. For this study, ω was set equivalent to 1.001.