Deductions for Unconnected Legs:

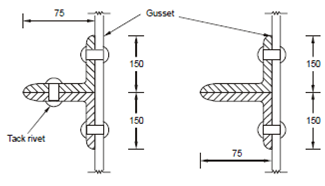
A tension member consist of two 150 × 75 × 10 mm IS angles, which are connected by their long legs to a 12 mm gusset plate by 16 mm diameter rivets (single row). Find out the net effective area of the angles under the following conditions:

(a) The angles are linked on the similar side of gusset plate and tack riveted.

(b) Same as (a) but without tack rivets.

(c) The angles are connected on opposite sides of the gusset plate and are tack riveted (Area of a 150 × 75 × 10 angle is 21.6 cm²).

(a) With Tack Rivets Connected to Same Side of Gusset Plate

(b) Without Tack Rivets Connected to Same Side of Gusset Plate

(c) Connected to Opposite Sides of Gusset Plate (with Tack Rivets)

Figure

Solution

Taking diameter of rivet hole = 16 + 1.5 = 17.5 mm

(a) Effective area of connected legs,

A₁= 2 × (150 - 17.5 - (10/2)) × 10 = 2550 mm²

Gross area of unconnected legs

A₂ = 2 × ( 75 - (10/2))× 10 = 1400 mm²

Factor k = 5 A₁/ (5 A₁ + A₂) =   5 × 2550/(5 × 2550 + 1400) = 0.901

∴ Net effective area = A₁ + kA₂ = 2550 + 0.901 × 1400 = 3811 mm²

(b) As the angles are not tack riveted they behave like single angles connected to gusset plate

Area of connected leg (single angle)

A₁ = (150 - 17.5 - (10/2))  × 10 = 1275 mm²

Area of unconnected leg (single angle)

A = (75 - (10/2))  × 10 = 700 mm²

∴ Factor k = 3 A₁/3 A₁ + A₂     = 3 × 1275/(3 × 1275 + 700) = 0.8453

∴ Net effective area of single angle = A₁ + kA₂

= 1275 + 0.8453 × 700 = 1866 mm²

∴ Net effective area of both angles = 2 × 1866 = 3732 mm²

(c) As in this case no deductions are to be made

∴ Net effective area = Gross area - Area of holes

= 2 × 2160 - 2 × 17.5 × 10 = 3970 mm²