BASICS OF ACO Or Ant Colony Optimization

By Dorigo, introduced Ant Colony Optimization or ACO is a meta-heuristic inspired by the foraging behaviour of ant colonies, where their objective is to recognize the shortest path among the nest and the food source? Ant Colony Optimization meta-heuristic is composed of various algorithms in which various cooperative agent populations try to simulate real ant behaviour. Throughout their movement, ants deposit a little amount of pheromone in the path moved that is a substance that may be smelled afterwards. Whilst ants arrive to the path intersection, they require choosing the path to follow. They choose this by applying a probabilistic decision biased by the amount of pheromone. Always, a stronger pheromone trail has been preferred by the ants.

After some time, mostly promising paths obtain a greater pheromone as compared to another one. This is because of the fact that, since these paths are shorter so the ants following them are capable to reach the goal rapidly and can begin their returning journey soon. As the time proceeds, each ant can direct its search or say so direct the search of the complete colony like a group as per to the amount of this pheromone on the ground.

Ethnologists determined that real ants, though blind, construct the shortest path from their colony to the feeding source via the employ of pheromone trails. The process is imitated in Ant Colony Optimization through the employ of a set of simple agents that is artificial ants which were assigned with computational resources and they exploit stigmergic communication that is a form of indirect communication mediated by the environment, to determine the solution to the problem at hand. Throughout their motion, ants drop specific amount of pheromone, a chemical substance utilized by ants to communicate and exchange information about that course to follow, on their chosen path hence marking this with a trail of this substance. The coming ant senses the pheromone on various paths and probabilistically chooses a path in accordance along with the probability that is directly proportional to the pheromone's amount upon it.

Throughout NC cycle for the k^th ant on node i, the selection probability of subsequently node j to follow is described by

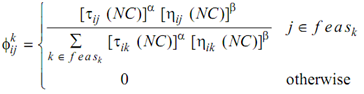
Here,

η_ij is a heuristic value called visibility on edge (i, j),

τ_ij(NC) is the pheromone's concentration at NC iteration,

α and β are the exponent parameters such control the relative significance of pheromone concentration versus the heuristic factors.

Hence, it is an autocatalytic process characterized by a positive feedback loop where the probability of selection of a path enhances along with the number of ants that decide the similar path. In order to ensure about the ants visit each the node, a special data structure called as tabu list is associated along with all ants. The tabu list saves the node previously visited and thereby forbids the ants to visit them once more. One time each ant completes their tours which is named as a cycle, the tabu list is utilized to find out the ant's solution value and thereby update the pheromone count on all edges. The pheromone strength on all paths is also decreased because of evaporation and is calculated utilizing a pheromone updation rule described as:

                                         t_ij (NC + 1) = (1 - ρ ) t_ij + Dt_ij................................Eq(2)

Here

                                                            Dt_ij =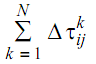..........................Eq(3)

And

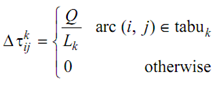                                            .........................Eq(4)

Algorithmic steps of basic ant colony optimization are displayed in Table no.2. Throughout begin of the new cycle, tabu list is emptied and the updated values give to guide the future path of ants. This procedure is iteratively repetitive for a designated maximum number of cycles, particular CPU time limit, or maximum number of cycles among two enhancement of the global best solution. Successfully the Ant Colony Optimization has been applied to solve a lot of complex NP-hard combinatorial optimization problems, as like: traveling salesman problem or TSP, vehicle routing problems, quadratic assignment problem and disassembly line balancing problem, to title a few.

                                      Table no.2: Algorithmic Steps of Basic Ant Colony Optimization

The method an ant selects the direction it must follow is easy, it gets any direction randomly, but ant's decision is biased by the pheromone amount in all possible paths. The continuous movement of every ant in the colony causes the best path, the faster ants go through it, and consequently more ants walk over the path and more pheromone is left behind. On the other hand, longer paths are progressively abandoned. At the conclusion, the best path or the minimum length one is found in between the ant nest and the food source. This mechanism is demonstrated in diagram.