Mutual Inductance:

Two circuits can be coupled magnetically as illustrated in Figure. Here coil1 and coil 2 have magnetic coupling in between them. Coil1 has N₁ number of turns and coil 2 has N₂ number of turns. Alternating source V_s establishes an alternating current i₁ which generates an alternating flux Φ₁ in coil1. Φ₁₁ is that portion of flux Φ₁ which completes its magnetic path around coil1 and the other part Φ₁₂ is the mutual flux linked with coil 2.

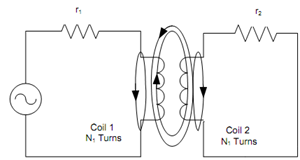
Figure: Magnetic Coupling

So,       Φ₁ = Φ₁₁ + Φ₁₂

The mutual flux Φ₁₂, which is alternating in nature, generates an induced e.m.f e₂ in coil 2 according to Faraday's law of electromagnetism,

                         e₂  = N (d φ₁₂/ dt )

Again e₂ is proportional to the rate of change of i₁, i.e.

e ₂ ∝ di₁/ dt

or,      e₂  = M₁₂    (di₁ /dt)

where M₁₂ is the constant of proportionality termed as mutual inductance between two coils. Its unit is Henry (H).

From Eqs. (13) and (15) we obtain,

N₂   (d φ₁₂/dt) = M₁₂ (di₁ /dt)

or,

M₁₂ = N₂ (d φ₁₂/ di)

The induced voltage e₂ generated in coil 2 causes alternating current i₂ to flow in coil 2. Current i₂ generates an alternating flux Φ₂ in coil 2. Out of flux Φ₂, a portion Φ₂₂ completes its path around the coil. The other portion Φ₂₁ is linked with coil 1 and it generates an induced e.m.f given by

N₁ (d φ₂₁ / dt) = M ₂₁ (di₂ /dt)

So, from Eq. (18), we obtain,

M ₂₁ = N₁ (d φ₂₁ /di₂)

If the flux and current are having a linear relationship which we consider to be true, Eq. (17) and Eq. (19) may be written as

M₁₂  = N2 (φ₁₂ /i₁)

and

M₂₁      = N₁ (φ₂₁/i₂)

Suppose that the permeability of the mutual flux path is constant, we have

M₁₂  = M ₂₁  = M