Remedial measures:

There are  two common approaches taken towards the problem of multicollinearity. First, 'do nothing' which is  simply  to ignore  the problem. Alternatively,  the researcher can follow some rules of thumb as outlined below. The order  in which the measures are given  here is  roughly by descending  order,of  their popularity. For instance, most researchers choose the  'do nothing' approach if there are no serious problenk  in interpreting the coefficients,  and so on.  

Do nothing :  Since multicollinearity is a problem with the data at hand, it is not possible to do anything about it, and therefore we try to make the most of existing situation.  In other words, it is a sample problem;  the sample available does not contain enough variation to,  identify certain impacts (for instance, if wealth  and  income always vary proportionately then the  impact of both separately  on consumption cannot be identified). Usually not all coefficients are statistically insignificant  in a regression model. Hence, we work with what we can get out of the model and hope that availablity of more data will allow a more accurate estimation  in future. Moreover, even if one or more  regression coefficients  cannot be estimated with great precision, a linear combination of them can be estimated relatively efficiently. For instance,  from equation above if we know that X₃=W₂,  then substituting  this into the equation we get

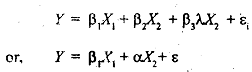
where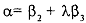. Note that  even if  we knew λ.  in the case of perfect collinearity, there is no way  to  get the  two cofficients  β,  and β,  separately. since we have one  equation with t  vo unknowns 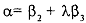.  Sometimes  we have to accept that this is the best that we can do given the data.