Perfect multicolinearity:
In the MLRM the parameter P, shows the impact of the explanatory variable (X1) on the dependent variable (Y). Therefore, estimated coefficients are the impact of each variable on Y, keeping all the other variables fixed at a particular level (say their sample mean levels). However, in the presence of perfect multicollinearity this is not possible since in the data (sample) used for estimating the model, there is a perfect correlation between the variables. In the example above there is a linear relationship, (X3 = 3X2). Therefore there is no way to estimate the impact of X3 on Y keeping X2 fixed, since in the data, X2 and X3 always change together. In other words we are seeking information that the data does not contain; this can arisi due to a number of reasons as discussed below. multicolinearity therefore often boils down to the fact that we are trying to answer a question that is not technically possible by using the data at hand.
For example, if we are trying to estimate the model:
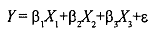
where is a random error term, y is the dependent variable, X,=l is the intercept . term, and X2, X3 are other explanatory variables. Let us say that we are trying to estimate the role that income and wealth of an individual play on the consumption expenditure incurred by the person in a given year. Suppose y is the consumption expenditure of individual r in year 2005, X2 is his income in that year, X3 is his wealth (total asset value) in the same year. Thus the model before us is
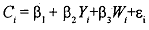
where C = consumption, Y = income and W= wealth. Here C is the dependent vaiable while Y and W are explanatory variables.
For the MLRM the estimated coefficients give us the intercept P, which is the level of consumption for someone with no income or wealth. P, gives us the change in consumption if income level for the person increases by one unit keeping his wealth level fixd (at the mean wealth level for the population). Similarly P3 gives the impact on consumption of a change in wealth level by one unit keeping his income fixed at the mean level. However, let us assume that after looking at'tbe data we come to realize that those with high incomes are also the ones with a higher wealth level. For simplicity let us assume that this relationship is perfect (linear), i.e., say the wealth level for each person is ten times the level of his current yearly income and this holds for all individuals surveyed (W=lOY). In order to find out how consumption expenditure of a person changes when income changes by a single unit keeping his wealth level fixed, intuitively the data needs to contain observations (people) with the same wealth level and different inComes. However this is not the case since in the data whenever income changes across individuals, the corresponding wealth ' level also changes proportionately (by a factor of ten).