Definition of Multicollinearity:

First we  take up the technical definition of multicdlinearity in the context of  the Multiple Linear Regression Model  (MLRM) and, then we will  discuss a mare intuitive explanation of what it actually means for the researcher. Multicollinearity refers to the presence of aperfect,  or exact, linear relationship among all or some of the explahatory variables in a regression. For instance if  x₁,...x_n,  (where X₁ = 1 is  the intercept term for all observations) are  the variables  being used in a regression, then an exact  linear relationship between them  is  said  to exist  if  the following condition  is satisfied:  

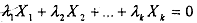
where  A₁,...,A_k are constants such that not  all of them are zero simultaneously. Equivalently we can say  that perfect multicollinearity  implies  that one of  the variables can be exrpessed as a linear combination of the others, as shown below.

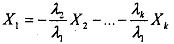
Exact  linear relationship, how ever, is a pathological case and it almost never arises in the  real world. This case also referred to as 'perfect multicollinearity'  is  therefore only usehl  for clarifying  the basic concept. In reality multicollinearity is commonly used to refer to a broader class of problems arising  in MLRM, such that:

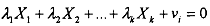
where v,  is a stochastic (random) error term, that varies across observations. Note that  for  this case it is not possible to express any  of the variables as a  linear combination of the other explanatory variable due to the presence of the random (and therefore indeterminate term) v,  for each observation. We will refer to this as the 'less than perfect multicollinearity' case. Although the implications of perfect multicollinearity are quite serious (see below),  technically  it  is also the least bothersome as will be shown below. The more pervasive type of less than perfect multicollinearity  that regularly arises  in empirical  studies  is also  technically  the more troublesome since  there is no easy way to avoid it.