Plane Motion of a Link:

A motion is called to be a plane motion if all the points in the body stay in the same and parallel planes. The concept of plane motion makes us able to consider only one of the parallel planes and analyse the motion of the points lying in that plane.

The parallel planes might not appear to be identical in size and shape but there is no problem because any plane of the body may be hypothetically extended through a mass less extension of the rigid body for the cause of kinematic analysis.

The mechanisms utilize links. Let a link PQ which is illustrated displaced in given Figure to position P′ Q′ in a common plane motion. The motion can be considered to include translation of an arbitrary point on the link as well as a rotation around an axis perpendicular to the plane & passing through that point. In an instance in figure eight combinations are equivalent.

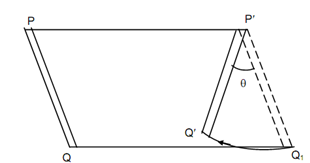
           Translation from PQ to P′Q₁ and Rotation around P′

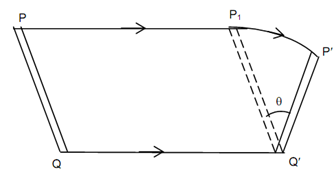
 Translation from PQ to P₁ Q′ and Rotation around Q′

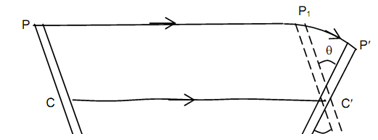
        Translation from PQ to P₁ Q₁ and Rotation around C′

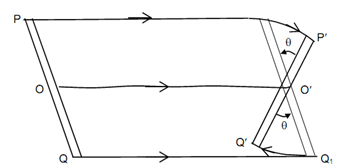
      Translation from PQ to P₁ Q₁ & Rotation around R′

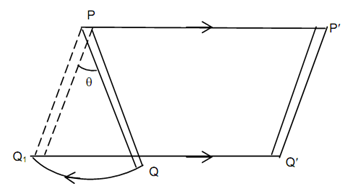
Rotation from PQ to PQ1 & Translation to P′ Q′

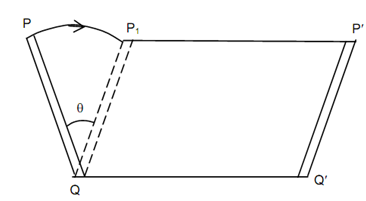
 Rotation from PQ to P₁Q & Translation to P′ Q′

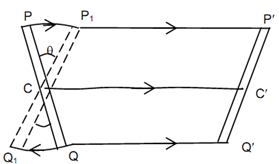
Rotation from PQ to P_i Q₁ & Translation to around P′ Q′

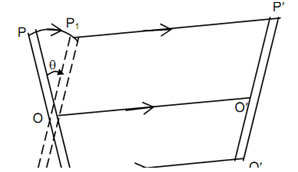
 Rotation from PQ to P₁ Q₁ & Translation to P′ Q′

The translation & rotation are commutative. In Figures (e) & (f) illustrate equal amount of translation and rotation but in Figures (a) & (b) translation is completed first and rotation afterwards. Likewise, Figures (a) & (e), (c) & (g), (d) & (h) are commutative.

It can also be noted down that, whatsoever be the mode of combination, the amount of rotation is similar. The angular velocity of each point on the link is the similar. Therefore, it is the customary to utilize the term angular velocity of the link instead of any specific point on it.

The fact that a general plane motion may be thought of like a superposition of translation & rotation is a special case of Chasle's theorem. In general the theorem states that any general motion of a rigid body may be considered as suitable superposition of a translational motion & a rotational motion.