Short-run Equilibrium:

In the short run, the monopolist cannot adjust it's plant size but it maximises its short-run profit by equating MR and MC. The second order condition required for equilibrium is that MC cuts MR from below.

Mathematical Derivation of the Short-run Equilibrium

Let the demand function in X=g(p) and the inverse demand function is P= f₁(X)
The cost function of the monopolist is given by C = f₂ (X). If  

Note that these conditions do not necessarily imply that monopolist can earn a profit. It depends upon the cost structure of the firm.

In the following figure, both the conditions MR= MC and MC cuts MR from below are met but the monopolist does not make any profit due to the cost structure.

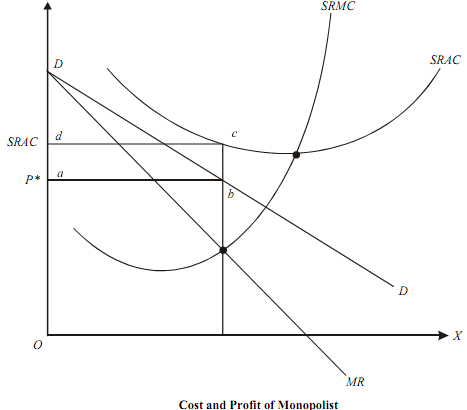
Here SARC (short-run average cost) > P*(equilibrium price) of the monopolist. The monopolist makes a loss of the amount given by the area, |abcd| .

The second order condition for profit maximisations is given by,

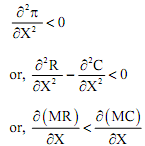
i.e., |slope of marginal revenue| < |slope of marginal cost|

The short-run equilibrium of a monopolist could be analysed graphically as well.

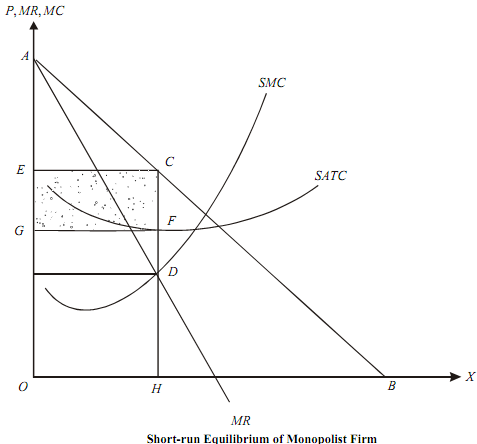
In the figure, AB is the demand curve of a firm and MR, the marginal revenue curve. The short-run equilibrium is given by the point D where SMC (short run marginal cost curve) cuts MR from below. The firm produces OH amount of output and sells it at price CH. Short-run average total cost of producing OH unit of the commodity is HF. Therefore, total profit of the firm is the area EGFC (shaded).

Thus, we can summarise the conditions of short run profit minimisation as

i) MR > MC

ii) MC cuts MR from below.