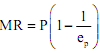Demand and revenue functions of a monopolist:

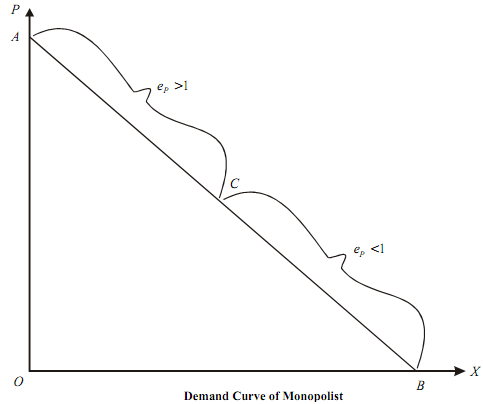
Since there is a single firm in the industry, the firm's demand curve is identical to the industry demand curve. Therefore, the demand curve of a monopolist in downward sloping. For the sake of simplicity in our analysis, we assume that the demand curve of a monopolist is a downward straight line.

Let the demand curve be given by  

X = a - bP ; a and b are positive
X: quantity demanded
P: price

The slope of the demand function is given by dP/dX = -1/b

The price elasticity at any point on the demand curve is given by

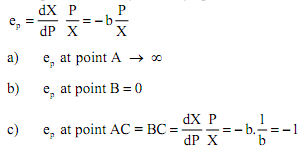
The total revenue of the monopolist is given by TR = P.X

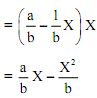
The average revenue (AR) is 

AR = TR/X = PX/X = P = a - bX

The marginal revenue (MR) is given by

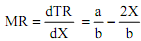
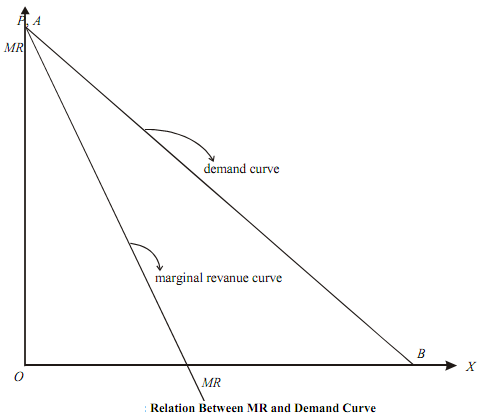
Clearly, the MR is a straight line having the same intercept as that of the demand curve but its slope is twice the slope of the demand curve.

The relationship between MR and price elasticity of demand (ep) is given by the following equation: