Potential Energy:

Look at the situation which is as shown in figure below. Whenever the object with mass m is increased through a displacement q, a force F is applied to it. Visualize what would occur when you let go of the rope and the object were permitted to fall.

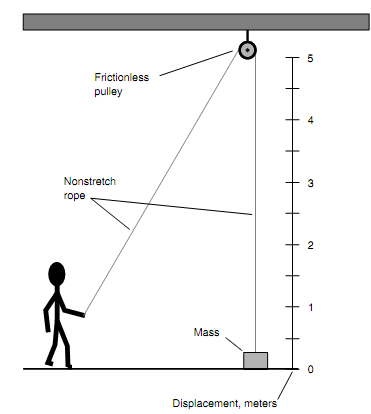
Figure: Work is done whenever a force is applied over a particular distance.

In this situation, the force is applied upward to an object against the Earth's gravity. Assume that m = 5 kg. This is around 11 pounds in Earth's gravitational field. Assume that the object is rigid and solid, like a brick. When you raise the brick a couple of millimeters, it will hit the floor without much fanfare. When you raise it 2 m, it will crack or dent a linoleum floor, and the brick itself may break apart. When you raise it 4 m, there will certainly be problem whenever it hits. The landing of a heavy object can be place to some helpful task, like pounding a stake into the ground. It can also do a lot of damage.

There is something about lifting up an object which gives it the ability to do work. This "something" is the potential energy. In mechanical sense, Potential energy is the same thing as work. When a force vector of magnitude F is applied to an object against Earth's gravitation and that object is lifted by a displacement vector of magnitude q, then Potential energy E_p is given by the formula as follows:

E_p = F_q

This is a naive view of potential energy. As we just discuss, potential energy can exist in a barrel of oil even if it is not lifted. The potential energy also exists in electrochemical cells, like the battery in your car. It exists in natural gas, gasoline, and rocket fuel. It is not as easy to calculate in those forms as it is in the mechanical illustration of figure above, though it exists nonetheless.

PROBLEM:

Look at the Figure as shown below. When the object has a mass of 5.004 kg and it is lifted 3.000 m, determine the potential energy it will achieve? Take the value of the magnitude of Earth's gravitational acceleration as a_g = 9.8067 m/s². We can neglect vectors here as everything occurs all along a single straight line.

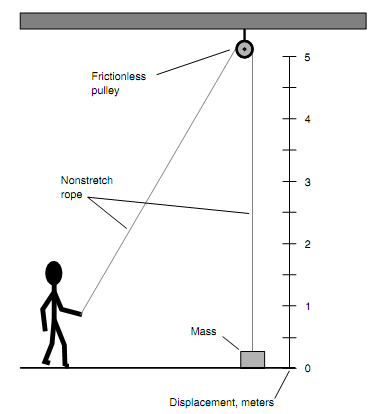
SOLUTION

At first, we should determine the force needed to lift a 5.004 kg object in Earth's gravitational field:

F = m_ag = (5.004 kg) (9.8067 m/s²) = 49.0727268 N

The potential energy is the product of the force and displacement:

E_p = F_q = (49.0727268 N) (3.000 m) = 147.2181804 J

We are allowed to go to four significant figures here since the least precise input data are given to four significant figures. Hence, E_p = 147.2 J.