Impulse:

Momentum of the moving object can change in any of three various ways as shown below:

- Change in the mass of the object

- Change in the speed of the object

- Change in the direction of an object's motion

Let us consider that the second and third of these possibilities altogether; then this constitutes a change in the velocity.

Imagine a mass, like a space ship, coasting all along a straight-line path in interstellar space. Think a point of view, or reference frame, therefore the velocity of the ship can be stated as a nonzero vector indicating in a certain direction. A force F might be applied to this vessel by firing a rocket engine. Visualize that there are numerous engines on this space ship, one planned for driving the vessel forward at raised speed and others capable of changing the vessel's direction. When any engine is fired for t seconds with force vector of F newtons as shown by the three illustrations in figure below, then the product Ft is known as the impulse. Impulse is a vector, represented by the uppercase bold-face letter I, and is stated in kilogram meters per second (kg . m/s):

I = Ft

Impulse generates a change in velocity. This is clear sufficient; this is the aim of rocket engines in a space ship! We have a formula concerning force F, mass m, and acceleration a:

F = ma

Replace ma for F in the equation for impulse. Then we obtain this:

I = (ma)t

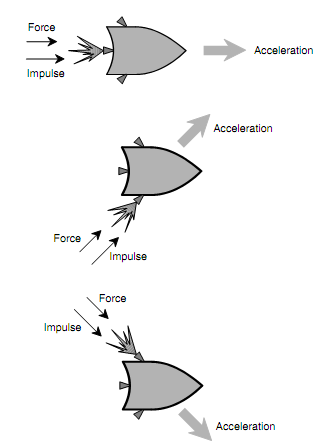
Figure: Three distinct ways in which an impulse can cause an object (in this situation, a space ship) to accelerate.

Now recall that acceleration is a change in velocity per unit time. Assume that the velocity of the space ship is v₁ before the rocket is fired and v₂ afterwards. Then, supposing that the rocket engine generates a constant force though it is fired,

a = (v₂ - v₁)/t

We can substitute in the previous equation to acquire

I = m[(v₂ - v₁)/t]t = mv₂ - mv₁

This means that the impulse is equivalent to the change in the momentum.

We have just derived a significant law of Newtonian physics. Summary to base units in SI, impulse is stated in kilogram-meters per second (kg . m/s), just as is momentum. You may think of impulse as momentum in the other form. Whenever an object is subject to an impulse, the object's momentum vector p always changes. The vector p can grow smaller or larger in magnitude, it can change the direction, or both these things can occur.

PROBLEM:

Assume that an object of mass 2.0 kg move at a constant speed of 50 m/s towards north direction. An impulse, acting at south direction, slows this mass down to 25 m/s, though it still moves in north direction. Determine the impulse for the change in momentum?

SOLUTION:

Initial momentum p₁ is the product of the mass and the primary velocity:

p₁ = 2.0 kg x 50 m/s = 100 kg . m/s

towards north direction. The final momentum p₂ is the product of mass and final velocity:

p₂ = 2.0 kg x 25 m/s = 50 kg . m/s

towards north direction. Therefore, the change in momentum is p₂ - p₁:

p₂ - p₁ = 50 kg . m/s x 100 kg . m/s = -50 kg . m/s

in north direction. This is similar as 50 kg . m/s in south direction. Since impulse is similar thing as the change in momentum, then impulse is 50 kg . m/s in south direction.

Do not let this outcome confuse you. The vector with magnitude -x in a certain direction is similar as a vector with magnitude x in the correct opposite direction. Problems at times will work out to result vectors with negative magnitude. Whenever this occurs, merely reverse the direction and then take the absolute value of the magnitude.