Bouncy Objects:

Now observe the figure which is shown below. The two objects contain masses m₁ and m₂, and they are moving at the speeds of v₁ and v₂, correspondingly. The velocity vectors v₁ and v₂ are not particularly shown here, though they point in the directions shown by the arrows. At A in this example, the two objects are on a collision course. The momentum of object with mass m1 is equivalent to p₁ = m₁v₁; the momentum of an object with mass m₂ is equivalent to p₂ = m₂v₂. Therefore far the case is just similar as that in figure shown below. Though here the objects are made of various stuff. They bounce off of each other whenever they collide.

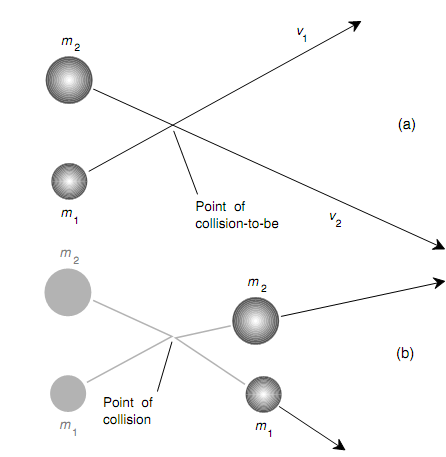
Figure: (a) Two bouncy objects, both with constant but dissimilar velocities, approach each other. (b) The objects after the collision.

At B, the objects have now hit each other and bounced. Obviously, their masses have not changed, though their velocities have, therefore their individual momentums have changed. Though, the total momentum of the system has not altered, according to the law of conservation of momentum.

Assume that the new velocity of m₁ is v₁a and that the new velocity of m₂ is v₂a. The new momentums of the objects are hence,

P_1a = m₁v_1a

P_2a =m₂v_2a

According to the law of conservation of momentum,

P₁+ P₂ = P_1a + P_2a

and hence:

m₁v₁ + m₂v₂ = m₁v_1a + m₂v_2a

The illustration shown in figure above represents idealized situations. In the real world, there would be difficulties which we are ignoring here for the sake of elaborating basic principles. For illustration, you may already be wondering whether or not the collisions shown in this drawing would impart spin to the composite mass (as shown in figure above) or to either or both masses (as shown in figure above). In the real world, this would generally occur, and it would make our computations vastly more complex. In this idealized illustration, we suppose that no spin is generated by the collisions.