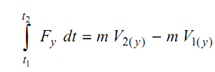Impulse-Momentum Equation:

If F_x is an applied force along with x direction on a body of mass (m) subjected to acceleration x¨  or d / dt  ( x? ) , then you shall recall that the Newton's Law of Motion states that,

F _x = m x¨ = m d ( x? ) /dt

where,  x  = distance traversed at any time t,

x?  = velocity along x direction at time t, and

x¨  =acceleration along x direction at time t.

Since mass (m) remains constant throughout its motion, we can write :

F_x  = d /dt  (m x? )

The product (m × x? ) is the momentum of mass (m) by virtue of its velocity (x ) at time (t).

If the applied force F_x varies with respect to time (t) as illustrated in Figure, the impulse

of the force F_x  during a short interval (dt) is the product (Fx  × dt ) given by the area of the

shaded portion LM M′ L′ illustrated in Figure.

∴ F_x dt     = { d/dt  (m x? )}dt

Integrating the effect of impulses throughout a period from (t₁) to (t₂ )

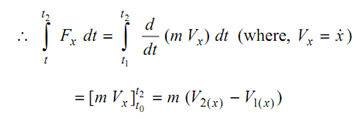
                         = m (V_{2( x )}  - V_{1( x )} )

where, V_{1( x )}  is velocity along x direction at time t₁, and

             V_{2( x)}  is velocity along x direction at time t₂.

Thus the integrated effect of impulse during time interval from t₁  to t₂  is the change of momentum of mass m along x direction. This is known as Impulse-Momentum Equation.

Similar equation may be written down in other two directions y and z. If Fy is the component of force along y direction and V₁( y ) and V₂( y ) are the velocities of the mass along y direction at time t₁  to t₂ , respectively, then