Perpendicular Axis Theorem:

Referring to Figure, whereas axis ZC is perpendicular to the plane of area A, we contain the polar moment of inertia of A around z-axis passing through C,

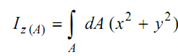
i.e., I _{z (A)}  =  I _{y (A)}  +  I _{x ( A)}

Moment of Inertia of the area A w.r.t. any axis X₁ X₁ shown in Figure is given by

I (X ₁X₁)  = ∫ dA × (square of distance from X1 X1 axis)

= ∫   dA × ( y +  y₁ )²

where, y₁ is the perpendicular distance between X₁ X₁ and CX. Therefore, for a given axisX₁ X₁, y₁ is constant.

Likewise,

I _{X 2 X 2}  = ∫ dA × ( y +  y2 )²