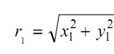Parallel Axis Theorem:
Referring to Figure it is noted that first moment of elemental area dA around centroidal axis is given by (dA × y). By the definition of centroid C of the area, further it is noted down that
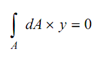
It means that horizontal plate of area A gets balanced around axis CX. While Moment of Inertia of areas are computed around any random axis X1 X1, then :
I (X1 X1 ) = ∫ dA ( y + y1 )2
= ∫ dA ( y 2 + 2 y y1 + y1 2 )
= ∫ dA × y 2 + 2 y1 ∫dA × y + y 12 ∫ dA
= I cx + 0 + A ( y1 )2
Likewise I (X1 X1 ) = Icx + A ( y2 )2
This equation is termed like parallel axis theorem whereby this is observed that out of all the axes parallel to centroidal axis, CX, the Moment of Inertia around the centroidal axis is minimum, for a given direction of the axis.
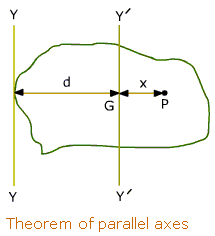
Likewise, Referring Figure,
I (y1 y1 ) = Icy + A ( x1 )2
Here x1 is the perpendicular distance between the axes Y1 Y1 and CY.
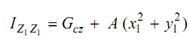
where the perpendicular distance between axes Z1 Z1 passing out through point K (x1, y1) and CZ is