Moment distribution method:

In the moment distribution method, therefore, we are not needed to solve any equations to determine the reaction etc. But we straight start searching the fixed end moments at all the joints and support points. After denoting the moments, the reactions can be found out by equations of statics. Here, the joints are assumed first to be all rigidly fixed; also without any translation (i.e. without horizontal movement or sway of any joint). A fixed end moment is first denoted for each member and then the joints are released for the sake of compatibility to attain equilibrium that is called balancing. This act of balancing results in introduction of carry over moments which cause loss of equilibrium again. Hence, a second balancing is associated, and then a second carry over and so on.

This process of repeated adjustments or balancing is carried out till we reach a point where sufficient accuracy of result is achieved. In fact we may stop at any point, as the process is a convergent one.

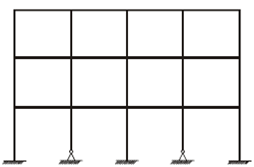
As you will very soon see that the method is quite simple and does not need solution of a number of simultaneous equations as is usually required for frames having a large number of redundancies. Figure 2 is a portal frame with 4 bays and 3 storeyes, having 12 beam members or 15 column members.

Figure

The number of joints is 20. As you can easily see that it has a large number of external unknown reactions, and internal unknown joint moments that is hard to solve without the use of fast digital computers. But it can be solved mechanically by the moment distribution method. The method was first proposed by Prof. Handy Cross in 1932 when digital computers and hand calculators were not available. Thus, by simple manual calculations fairly accurate results could be obtained.