Distribution Factor:

The procedure of moment distribution could be explained by the following example of a redundant joint :

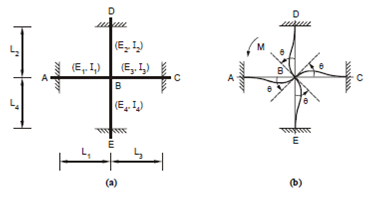
In Figure 7(a), four bars AB, DB, CB and EB are meeting at joint B, which is a rigid joint (not hinged).

Also the ends A, D, C, E are fixed-ended supports. The modulus of elasticity, moment of inertia and lengths of the bars are (E₁, I₁, L₁), (E₂, I₂,L₂) etc as shown.

Now if the bars AB, BC, etc. are loaded by transverse loads fixed ends moments (FEM) develop at both ends of each bar. Thus, bar AB will have M_FAB and M_FBA as fixed end moments at ends A and B respectively? Finally, at the joint B we will have four fixed end moments M_FBA, M_FBD, M_FBC and M_FBE that might have their own magnitudes and sign [clockwise (+) or anticlockwise (-)].

For statical equilibrium of the joint B and the algebraic sum of all the moments must be zero. If it is not zero a balancing moment M has to be applied such that

 [M _FBA+ M _FBD + M _FBC + M _FBE ] + M = 0

Now the balancing moment M will cause a rotation at the joint so that each member will rotate through an angle θ. That rotation will be the similar for all the members as the joint 'B' is a rigid one and angles between the bars cannot change. This is shown in Figure 7(b). However, this rotation θ will introduce a moment at each of the member ends at B.