Continuous Beams:

Now, that will be explained through an example of a continuous beam given below.

Moment Distribution Method Applied to Continuous Beam

Example

A continuous beam fixed at ends A and D is loaded as shown in Figure 8. The end spans AB and CD have moment of inertia I and for the middle span BC the moment of inertia is 1.5 I.  It determines the moments and reactions at the support and draw the BM and SF diagrams.

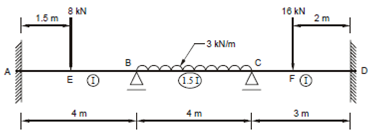
Figure 8

Solution

Step 1 The fixed end moments for each member is determined below:

Member AB   M_FAB = 8 × 1.5 × (2.5)²/4² =-4.6875 kNm

M_FAB = 8 × (1.5)² × 2.5/4² =-2.8125 kNm

Member BC M_FAB = 3× 4²/12 =-4.0 kNm

M_FCB = 3× 4²/12 = +4.0 kNm

Member CD M_CD =16x1x2²/3² = -7.1111 kNm

M_CD =16x1²x2/3² = +1.7778 kNm

Step 2

A distribution factors for members meeting at each joint are determined below:

At joint A

A joint A is fixed and there is just one member AB, hence, no distribution is required here.

At joint B

The joint B is easily supported and two members BA and BC meet at this joint

K _BA = I/ l = I/4

K _BC     = 1.5 /I

∴          By Eq. (3.16), distribution factor for BA,

=  K _BA/∑ K = (I/4)/((I/4)+(1.5 I/4)) =0.4

Distribution factor for BC, = K _BA/∑ K = (1.5I/4)/((I/4)+(1.5I/4)) =0.6

At joint C

There are two members CB and CD and we have K_CB   = 1.5 I/4

And K_CD =I/3.

and DF_CB =(1.5I/4)/((1.5I/4)+(I/3)) =0.53

and DF_CB =(I/3)/((1.5I/4)+ (I/3)) =0.47

At joint D

Since the joint is fixed there will not be any distribution of moment at the only member DC meeting at this joint (DF = 0).

The actual process of distribution of moments begins. This is usually done in a tabular form. Various authors have suggested various forms. To facility of compute for a continuous beam the simple scheme in Table appears to be good enough.