Calculate the slopes at the supports:

Using the moment area theorems calculate the slopes at the supports and at midpoint, and the deflection at the midpoint of the beam shown in Figure. EI (= 6000 kN m²) for the beam is constant.

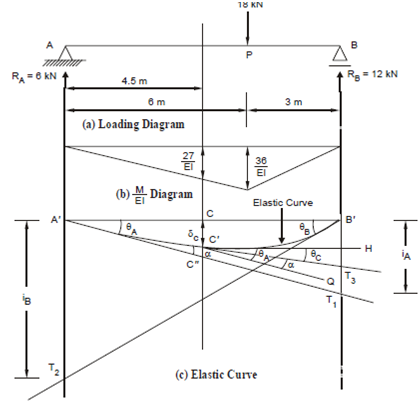
Solution

The reactions at A and B can be calculated as

R_A   = (18 × 3)/9 = 6 kN

R_B   = (18 × 6)/9 = 12 kN

The BM diagram is a triangle with apex at P, M_P= (18 × 6 × 3)/9 = 36 kNm . As EI is constant, the M/EI   diagram is a similar triangle with maximum ordinate at P = 36/EI . This is shown in Figure 2.10(b). The ordinate below the midpoint C = 36/EI × 4.5/6 = 27/EI .

The deflected shape of the beam (the elastic curve) is shown in Figure 10(c).

A′T1 and B′T2 are tangents to this curve at supports A and B respectively. The tangent through C′ is C′T3. A line C′Q is drawn parallel to A′T1, then ∠ HC′Q = θ A .

Let ∠ T3C ′Q = α , then slope at C ′ = ∠ HC ′T3 = θC= θ A- α .

The vertical through C meets the elastic curve at C ′ and tangent at A′T₁ at C ′′.

The deflection at C, δC  = CC′ = CC′ - C′C′ .

By second moment area theorem, intercept B′T1 = Moment of the entire M/ EI area about BB′, i.e.

i_A =((36/EI)x(9/2))x((0+3+9)/3) = 648/EI

Now, because θ_A is small

θ_A  ≈ tan θ _A = i_A/9 =648/9EI =72/EI =72/6000 radians =0.012 radian =0.688^o

Similarly, θB is obtained by taking moments of the M/EI area about A

i_B =A'T₂= ((36xEI)x(9/2)x((0+6+9)/3) = 810/EI

∴  θ_B= i_B /9= 810/9x6000 =0.015 radians =0859^o

Now, from the diagram α is the difference of the slopes between A and C and by first moment area theorem, it is equal to the and C. M/EI   area between A and C

 α = 27/EI × 4.5/2 = 60.75/EI

∴ Slope at C, θ_C = θ _A - α = 72/EI - 60.75/EI = 11.25/EI = 11.25/6000 radians = 0.107^o.

Now deflection at C, δC = CC′ = CC ′ - C ′C′.

Here, CC′= AC × θ_A= 4.5 × 72/EI= 324/EI

and     C′C′′ = intercept between tangents at A and C at a line passing through C.

= moment of M/EI   area among A and C about C (by second moment area theorem).

 =((27/EI)x(4.5/2))x4.5/3=91.125/EI

∴ δ = 324/EI - 91.125/EI = 232.875/6000 = 0.0388 m = 39 mm (approx.)