Uses and limitations

Specifying the point group is a helpful way of summarizing specific aspects of the structure of a molecule: for instance the C₃v symmetry of NH₃ involves a pyramidal structure as different from the planar D₃h molecule BF₃. Though, it must be recognized that specific significant features are not implied by symmetry alone. Even molecules with distinct stoichiometry may have similar symmetry elements, for instance BF₃ and trigonal bipyramidal PF₅ share the D₃h point group. The C₃v point group tells us that three N-H bonds in ammonia are equivalent but says nothing about their actual length.

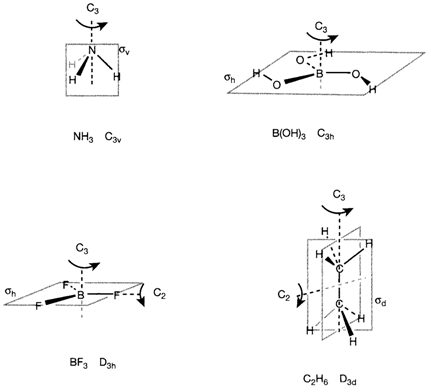
Symmetry may be helpful for predicting molecular properties. The instance of chirality has been discussed before. Other example is polarity resulting from the unequal electron distribution in polar bonds. The complete polarity of a polyatomic molecule occurs from the vectorial sum of the contributions from every bond and is zero if the symmetry is too high. With a net dipole moment, a molecule can have no inversion center and at most one rotation axis and any reflection planes exist must consist of that axis. The only point groups well-suited with these needs are C₁, C_s, C_n, C_nv and C_∞v. So, of the molecules displayed in diagram 3, only NH₃ can have a dipole moment.

Advanced applications of symmetry imply the behaviour of molecular wavefunctions under symmetry operations. For instance in a molecule with a centre of inversion (like a homonuclear diatomic, see Topic C₄), molecular orbitals are categorized as u or g (from the German, ungerade and gerade) as per to the whether or not they change sign under inversion. In ligand field theory  the t_2g and e_g categorization of d orbitals in an octahedral complex relates to their behavior under the symmetry operations of the Oh point group. Molecular vibrations may be categorized in identical ways and such type of analysis can be valuable in using vibrational spectroscopy to determine the point group of a molecule.