Point groups

By performing two symmetry operations in sequence generates other symmetry operation.  For instance, two sequential C₄ operations about similar axis make a C₂ rotation; reflecting twice in similar plane gives the identity E. Each symmetry operation  also has an inverse operation  which reverses its influence. For instance, the inverse of a reflection is similar reflection; the opposite of an anticlockwise C₄ operation is a clockwise rotation about similar axis. These properties denote that the complete set of symmetry operations on a given object form a mathematical system termed as a group. Point groups are the groups of symmetry operations of molecules, in distinction to space groups that are involved in crystal symmetry and involve operations of translation, shifting the one unit cell into the position of another.

Chemists make use of the Schönflies notation for molecular point groups, the labels employed being listed in the 'flow chart' displayed in Fig. 2 and described below.  For a non-linear molecule with at least one rotation axis, the first significant question is whether there is a principal axis, a exclusive Cn axis with highest n. For instance SF₆ has no principal axis, as there are various C₄ axes. The molecules displayed in Fig. 3 though all have a principal C₃ axis as there is no other of similar type. Given a principal axis, the only another axes allowed are C₂ axes perpendicular to it called as the dihedral axes. Point groups with and without such type of axes fall into the general classes Dn and Cn, respectively. These are additionally specified If there are reflection planes,. A horizontal plane (σh) isoneperpendicularto the principal axis, so being horizontal if the molecule  is oriented so that the axis is vertical. The molecules B(OH)₃   and BF₃ in diagram 3 do have a σh plane and

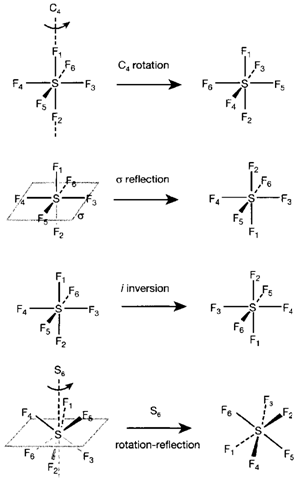
Fig. 1. Symmetry operations and elements demonstrated for SF₆  The effect of each operation is shown by the numbering of the F atoms.

have the point groups that are C₃h and D₃h, correspondingly. In a Cn group,  planes which consist of the principal axis are known  as vertical and give the point group Cnv, for instance C₃v for NH₃. Though, in a Dn  group without a horizontal plane, any planes consisting of the principal  axis lie between the dihedral axes and are called diagonal thus giving the point group Dnd (instance D₃d for the staggered conformation  of ethane as shown  in diagram 3). Dnd groups can be hard to identify since the dihedral axes are hard to see.

Linear molecules fit into the above categorization by using the designation C∞ for the molecular axis involves that a rotation of any angle whatever is a symmetry operation. 

So, we have C∞v for a molecule with no centre of inversion (instances being CO and N₂O) and D∞h if there is an inversion center (instances being N₂  and CO₂),  the existence of such type of a center implying  also that there are dihedral axes.

If there are various equivalent Cn axes of highest n, the designation rely on n. Groups with n=2 are of type D₂; generally there are also reflection planes and an inversion center giving D₂h (for instance, C₂H₄). With n=3 we have tetrahedral groups (T), the most common instance being Td, the point group of a regular tetrahedral molecule like CH₄  with reflection planes but no inversion center. The Octahedral groups (O) take place with n=4, most frequently having an

Fig. 2. Flow chart for identification of point groups.

Inversion center giving Oh (example SF₆, Fig. 1). The highest Cn allowed with no a principal axis is n=5 giving icosahedral group I.