Calculate Modular Ratio:

Let the whole axial force applied on the composite member P be shared by the different members as P₁, P₂ and P₃. If the deformations produced are δ₁, δ₂ and δ₃, then we obtain,

δ ₁  =   P₁ L₁ / A₁E₁

δ₂   =   P₂ L₂  / A₂ E₂

δ₃ = P₃ L₃   / A₃ E₃

The compatibility condition needs that

 P₁L₁/ A₁E₁ = P₂ L₂/ A₂ E₂ =  P₃ L₃/ A₃ E₃

Let the elastic modulii of the materials be redefined as E₁, m₂ E₁ and m₃ E₁, where

m₂ =   E₂/ E₁  and  m₃ = E₃/ E₁

Eq. (7) might be rewritten as follows

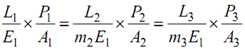
(L₁ / E₁)× (P₁ /A₁) =L₂/(m₂E₁) ×( P₂ /A₂) = (L₃/ m₃ E₁)   × (P₃ /A₃)

Recognising that L₁ = L₂ = L₃, we might rewrite Eq. (8) as

P₁/ A₁   = P₂ / (m₂ A₂ ) =          P₃ / (m₃ A₃)

 from which, we obtain P₂ =    (P₁/ A₁ )m₂ A₂ and

          P₃ = (P₁ / A₁ )m₃ A₃

 The equilibrium condition needed to be satisfied is

P₁ + P₂ + P₃ = P

or         P₁  +( P₁/ A₁) m₂A₂   +   (P₁ /A₁) m₃ A₃ = P

P₁ (1+(m₂A₂/A₁) + (m₃A₃/A₁)) =P           m A

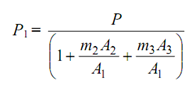
After calculating P₁ by using Eq, the loads shared by other members P₂ and P₃ might be calculated utilizing the Eq.

In the procedure of the above solution, we have introduced two terms, as, m₂ and m₃ whose values are the ratios (E₂/ E₁) & E₃/E₁ respectively. These ratios refer to  the ratios of

Elastic modulii of two different kind of materials and, hence, are called as Modular Ratios.