Dynamic or Autoregressive Models:
Lquations similar to may also be obtained directly by postulating dynamic or autoregressive models, i.e., models with lagged dependent variables on the right hand side of the equation along with the usual explanatory variables.
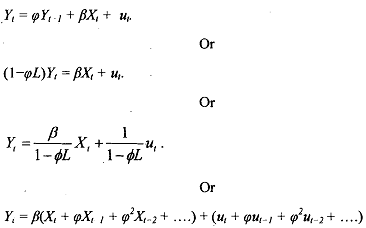
Thus, the dynamic model with a lagged dependent variable gives rise to precisely the same geometric distributed-lag schemes as does the Koyck model. However, the two models differ in the nature of the disturbance term. The Koyck model has a standard white noise disturbance term while the dynamic model has an autoregressive disturbance term.
Notice that the dynamic model, discussed above, implicitly assumes that the dynamics of the disturbance term are the same as the dynamics of the system (the parameter in both cases is φ). This can lead to biased and inconsistent estimates of φ if the true coefficient of ut- 1 in is in fact different from φ. Remember that φ represents the system dynamics and helps in estimating the speed of the response or adjustment. Thus, misspecification may lead to wrong inferences about the speed of the response.