Distributed Lag Models:
In other words, the effect of an event may be distributed over several time periods. Fo~.example, firms do not rush to increase investment unless they see a sustained increase in sales. A one time increase in sales because of an unexpectedly harsh winter or a natural calamity will not see firms increasing investment expenditure and expanding productive capacity. Similarly, investment in new equipment (Xt) in period t may impact profit (Y,) over several periods, βoXt in period t, βiXi, in period t+l, and so on up to βiXi, in period t+s. This may be expressed as
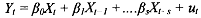
Given that the usual Gauss-Markov conditions1 hold this model may be estimated by ordinary least squares. However, there are several questions/problems that arise, some of which are particularly important. First, how do we decide on the length of the lag structure? Should it be finite or infinite? Theory is usually silent on this matter. Further, too short a lag structure may lead to inaccuracies and too long a lag structure may result in a model with very few degrees of freedom.
Secondly, the lagged values of X are likely to be highly correlated resulting in imprecise coefficient estimates (large standard errors) and making inference difficult.
Thirdly, what will be the response structure or the lag structure? Usually an assumption is made that all the coefficients will have the same sign, i.e., the impact of the event will be monotonic in nature. In other words, investment in new equipment today will either increase profit for the next periods or decreage profit' for the next s periods. Specifically, we do not allow for the case that it may decfease profit for the next five periods and then increase it from period six to s. It is also usual to assume that the impact of the event will decline in magnitude over time (the coefficients will decline in absolute magnitude to zero) although there may be a short initial period when the absolute magnitude of the coefficients increases. The assumption, while not always realistic, is necessary for ease of estimation.
The need to economize on the number of coefficients has led to the development of different lag schemes, essentially different assumptions about the weights (coefficients) β0, β1,. . . .βs.
De ~eeuw* advocated the use of an inverted V structure for the weights. In a total lag of s periods, the first half of. the weights are taken as proportional to the increasing series 1,2,3,. ... s/2, and the second half of the weights are chosen
proportional to the weights s/2, (s/2 - 1),. . . ..3,2,1.
A few years later Almon3 suggested a more flexible approach. He suggested (using the Weierstrass theorem) that the actual lag function could be approximated by a polynomial of suitable degree4. The estimation of the model can be done by least squares as the Gauss Markov conditions are satisfied.
In both the above approaches the total lag period is finite and has to be specified prior to estimation. The biggest problem in using models with finite lag structures is: How do we determine the length of the lag? There are no easy answers to this question and consequently the emphasis has been on infinite lag models.