Separating Equilibrium:

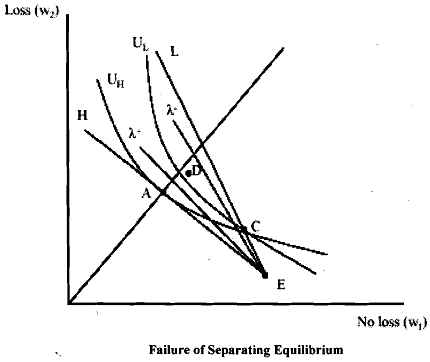
We have seen above that the pooling equilibrium is not feasible. Therefore, let us  consider  a  'separating  equilibrium'  instead. For  that  purpose,  it will be useful  to  examine Figure.  In  the  figure we have Just  as  in  case  of the pooling equilibrium two  fair odds line corresponding  to the two different risk groups. Points AL  and AH  give full-insurance points for  the two  risk groups. Group  I,  has higher wealth because its odds of experiencing a loss are lower. In the figure, C on the fair odds line is for the L group. The indifference curve from the full-insurance point for the H group crosses the fair odds line for the group L at this point. Moreover, the indifference curve U1*  that intersects point C  is  steeper than  the corresponding  curve for  the  group H.  Thus, we have  

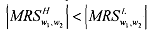
as has been shown earlier.

On the basis  of  the Figure,  we  can make the following observations concerning the two groups, H and L:

i)  C  is  the best policy the  insurance company could offer  to  the L types that would not at the same time attract H types.

ii)  If the company offers the policy C+  on the figure to L types, they would strictly prefer it. However, the problem with it is that H types would also  prefer  it. Such a policy therefore would produce a pooling equilibrium.

In  addition, C+  involves cross-subsidy  if H types take it because UH  is the indifference curve for the fully-insured type H. If there is a point that H  types prefer  to  full-insurance, it  can  only mean  that  the policy  is subsidised.

iii)  If the company offers a policy C-, H types would not select it. With such an offer,  L  types  would strictly prefer  the  original policy,  C.

Consequently,  any policy like C- will be dominated by C. So, C  in  the  figure  defines  the 'separating  constraint' for  types H,  L.  Any other policy  that  is more  attractive  to  H  types would result in  pooling.  In equilibrium, we get policies AH  and C where type H  chooses AH  and type L chooses C. Both policies break even since each lies on  the  fair odds line for the insured group. In the equilibrium H risk types are fully insured and L risk types are only partly insured.

It  is important to note that equilibrium arrived in the market is influenced by the  preferences of  H risk  buyers.  The insurance providers maximise  the welfare of L risk buyers subject to the constraint that they don't attract H risk buyers.  Despite the  constraints imposed by  the H  risk  types on L risk types, they are not  better off.  You have a solution where one group loses without gains to the other.