Case of Homogenous Risk Pool:
Let us start with the simplest case to see how it works. Assume that all potential insured have the same probability of loss, p : pi = p for all i and as we have already assumed that all losses are equal to d. See Figure, which presents the state preference diagram taken from risk aversion and insurance discussed earlier. Note that from the initial endowment E = (w, w - d) , the fair odds line extends with slope -(1-P)/P, reflecting the P odds ratio between the accident and no-accident states. As we have shown a risk averse agent will optinlally purchase full insurance. Following from the von Neumann-Morgensteni expected utility property, the highest indifference - curve tangent to the fair odds line has slope -(1-P)/P at its point of tangency with the fair odds line, which is where it intersects the 45' line. At this point, wealth is equalised across states. So, the tangency condition yields
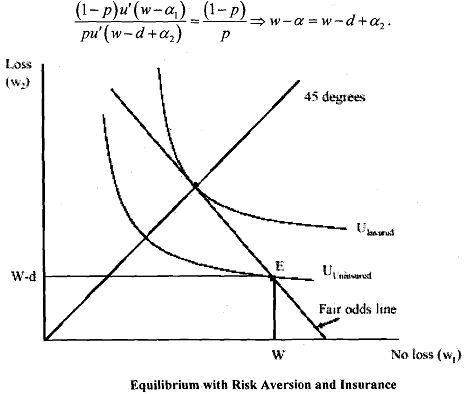
In this simple case, insurance companies will be willing to sell the policy α = (pd, (I-p)d) since they break even. It is also important to note that when the above tangency condition is satisfied, there is no alternative profit-making policies that could potentially be offered.