Step 1:

Substituting Eqs. (10.8) and (10.9) in (10.1), we get cost per component in terms of speed and feed.

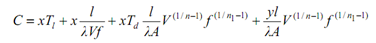
Step 2:

Following two cutting conditions should be satisfied to get minimum cost per component (i.e., to get optimum cutting speed and optimum feed).

∂C/∂V = 0                      --------------- (11(a))

∂C/∂f = 0                       ---------------------(11(b))

Partially differentiating Eq. (10.10) with respect to cutting speed V, we get,

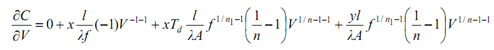
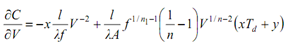--------(11(c))

Using Eq. (10.11(a)), we may write Eq. (10.11(c)) as :

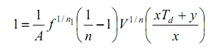
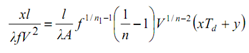
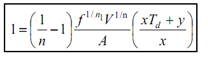                    ------------ (12)

Equation (12) gives the condition to determine optimum cutting speed.

 Now, after partiatially differentiating Eq. (10) (i.e., ∂C/∂f  = 0 ) with respect to  f, we get

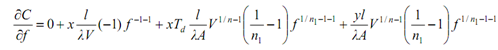
or,

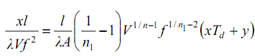
or,

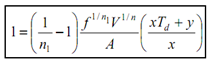           --------------- (13)

Eq. (13) gives the condition to determine optimum feed rate.

Eqs. (12) and (13) cannot be satisfied simultaneously and unique minimum does not occur.