By Limiting Minimum Number of Teeth on the Pinion:

Given fig illustrates meshing of two gears. Motion is transferred through pinion to the gear. AB is tangent to the base circles. Theoretically specking, the addendum circles of pinion and gear may respectively pass through A and B. hence,

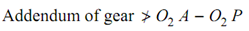
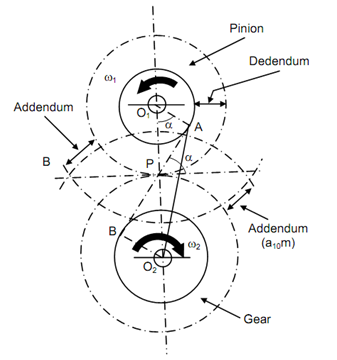
Assume number of teeth on gear and pinion respectively be T & t. Assume m be the module of the gears that has to be similar both pinion and the gear.

O₂ P = T_m /2      on   O₁ P =   m t/2

and gear ratio 'G' = T /t.

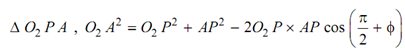
Thus, O₂ A₂ = O₂ P₂ + O₁ P₂ sin ² φ + 2O₂ P × O₁ P sin ² φ

 putting for O₁ P and O₂ P.

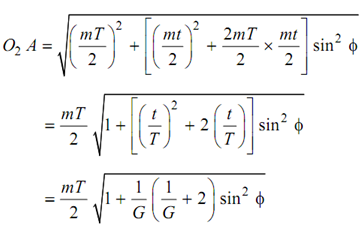
Thus, addendum of gear

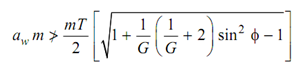
here a_w is the multiplying factor for gear.

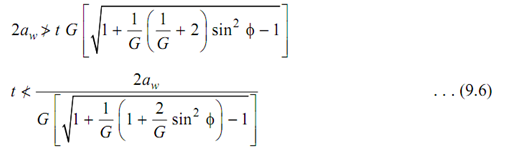
all have stronger root due to cycloidal profile at the root.