Find out acceleration:

In a slider crank mechanism illustrated in Figure, the crank OA rotates at 600 rpm. Find out acceleration of slider B while crank is at 45^o. The lengths of crank OA & connecting rod AB are respectively 7.5 cm and 30 cm.

Solution

The angular velocity of crank OA,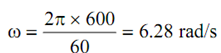. The crank OA is a rotating body around fixed centre O. Thus, the velocity of point A is illustrate by

                              V_A = ω× OA = 6.28 × 7.5 = 47.1 cm/s or 0.471 m/s

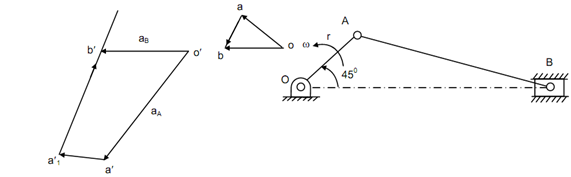
Select appropriate position of pole o that represents fixed reference. Draw a line oa perpendicular to OA to represented velocity of A that means V_A in magnitude and direction. From point a, draw a line perpendicular to AB to signify direction of relative velocity V_BA. Now draw another line which should be parallel to the motion of the slider B from O to signify direction of the velocity of slider V_B to meet another line by a at b. Therefore ob shows velocity of B in magnitude and direction.

As crank OA rotates at uniform angular speed, thus, acceleration of A shall be centripetal acceleration.

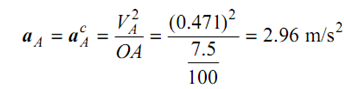
It is directed from A to O.

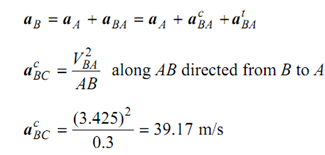
Choose a suitable position of pole O that represents fixed reference. Plot acceleration of A that means A by drawing parallel to OA and demonstrating its magnitude by an appropriate scale. It is signified by o′a′. Now, draw a line from 'a′' parallel to AB for ac and demonstrate its magnitude. This is represented through a′a′1. Now from a′1 draw a line perpendicular to a′a′1 or AB to signify direction of . Draw a line from o′ parallel to the motion of slider B to show direction of motion of B. This line from o′ will meet another line from a′₁ at the point b′. The acceleration of slider B is showed by o′b′ in magnitude and direction and it gives a_B  = 215 m/s²