Angular acceleration of link:

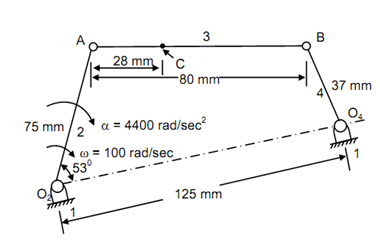
A four bar chain O₂ AB O₄ is illustrated in fig. The point C is on link AB. The crank O₂A rotates in clockwise sense having 100 rad/s and angular acceleration 4400 rad/s². The dimensions are illustrated in Figure (a). Conclude acceleration of point C and angular acceleration of link O₄B.

                                           (a)

                               (b)

           (c)

Solution

First Draw configuration diagram to the scale.

The velocity of point A, V_A = O₂ A × ω = 1000 × 100 = 7.5 m/s

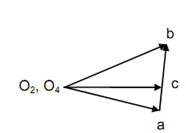
Velocity Diagram

For drawing velocity polygon the given steps might be followed as:

 (1)       Suppose suitable scale say 1 cm → 5 m/s.

(2)        Plot velocity of A, V_A perpendicular to O₂A. It is illustrated by o₂a in velocity polygon Figure (b).

(3)        Draw a line from point a perpendicular to AB to signify direction of V_BA.

(4)        Draw a line from o₂ perpendicular to O₄B to signify direction of V_B to meet line demonstrating direction of V_BA at b. o₂b represents V_B in magnitude & direction.

(5)        For finding velocity of C, plot point c on ab such as

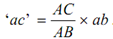
From velocity polygon and

V_BA  = 6.5 m/s

V_B  = 9 m/s

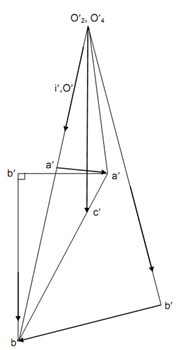
For drawing acceleration polygon, the given steps might be followed:

 (1)       Acceleration of A that is 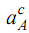 = O₂ A ω₂ . Or

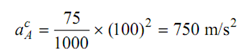. A scale 1 cm → 250 m/s may serve the cause.

(2) Draw a line parallel to O₂A & plot ac that will be given 3 cm. this is represented by o2′ a1′ in polygon.

(3) Draw a line perpendicular to O₂A from a′1 in the sense of angular acceleration to signify tangential acceleration which is 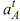 = O₂ A × α = (75/100) × 4400 = 300 m/s².