Black's Models:
 
Duncan Black has explained three types of cases for the translation of individual preferences in terms of collective choice.
 
i)  Single peaked preference with odd number of voters.
ii) Single peaked preference with even number of voters.
iii) Non-single peaked preference pattern.
 
Figure explain case (i) and (ii) respectively. 

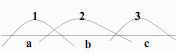
Suppose there are three (odd number) of voters. If there is comparison between (a, b) and (b, c) through majority rule in Figure 6.6 which gives the preference pattern of all individuals as single peaked then option b wins and it is the preference of individual 2. Here individual 2 is the median voter.

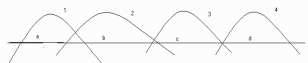
In Figure 6.7 there are four (even number) of voters.  The preference pattern of all the voters are single peaked 'b' wins over  'a' and 'c' wins over 'd' through majority rule.  However comparison of (b, c) through majority rule gives indeterminate result.  Therefore in this case either voter 2 or voter 3 will be allowed to give an extra vote and accordingly the median voter preference will be determined.
 
If there are  'n' discrete numbers in ascending or descending order median value is 

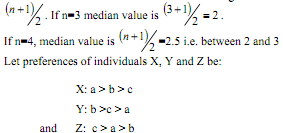
This type of orderings give non-single peaked preference pattern as illustrated in 6.2.1. In this case it is difficult to identify the Median Voter.  Its solution is given in terms of sequence in voting applying the Majority rule. 

Compare (a, b), a wins then compare (a, c), c wins
Compare (b, c), b wins then compare (b, a), a wins
Compare (a, c), c win then compare (c, b), b wins
 
Therefore finally whether a or b or c  wins in collective  choice depends on the sequence of voting and accordingly X or Y or Z will be the median voter.