Convection Heat Transfer

Convection includes the transfer of heat by the motion and mixing of "macroscopic" sections of a fluid (which is the flow of a fluid past a solid boundary). The word natural convection is employed when this motion and mixing is caused by the density variations resultant from temperature differences in the fluid. The term forced convection is employed when this motion and mixing is caused by an exterior force, like a pump. The transfer of heat from a hot water radiator to a room is an illustration of heat transfer by natural convection. The transfer of heat from the plane of a heat exchanger to the bulk of a fluid being pumped via the heat exchanger is an illustration of the forced convection.

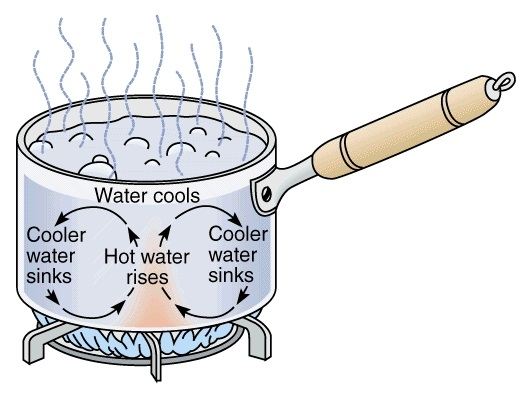
The heat transfer by convection is harder to examine than heat transfer by conduction since no single property of the heat transfer medium, like thermal conductivity, can be stated to explain the mechanism. The heat transfer by convection differs from condition to condition (ahead the fluid flow situation), and it is often coupled with the form of fluid flow. In practice, study of heat transfer by convection is treated empirically (by direct surveillance).

The convection heat transfer is treated empirically since of the factors which affect the sluggish film thickness:

• Fluid velocity
• Fluid viscosity
• Heat flux
• Surface roughness
• Kind of flow (single-phase/two-phase)

The convection includes the transfer of heat among a surface at a given temperature (T_s) and fluid at a bulk temperature (T_b). The exact definition of the bulk temperature (T_b) differs based on the details of the condition. For flow adjacent to a hot or cold surface, T_b is the temperature of the fluid "far" from the surface. For condensation or boiling, T_b is the saturation temperature of the fluid. For the flow in a pipe, T_b is an average temperature calculated at a specific cross-section of the pipe.

The fundamental association for heat transfer by convection has similar form as that for heat transfer by conduction:

Q - h A ΔT

Here:

Q = rate of heat transfer (Btu/hr)  

h = convective heat transfer coefficient (Btu/hr-ft²-°F)

A = surface area for heat transfer (ft²)

ΔT = temperature difference (°F)

The convective heat transfer coefficient (h) is reliant upon the physical properties of the fluid and the physical condition. Usually, the convective heat transfer coefficient for laminar flow is associatively low compared to the convective heat transfer coefficient for turbulent flow. This is due to turbulent flow containing a thinner stagnant fluid film layer on the heat transfer surface. Values of h have been calculated and tabulated for the usually encountered fluids and flow conditions taking place throughout heat transfer by convection.

Most of the applications including convective heat transfer occur inside pipes, tubes, or some similar cylindrical device. In such situations, the surface area of heat transfer generally given in the convection equation (Q - h A ΔT) differs as heat passes via the cylinder. Additionally, the temperature difference existing among the inside and the outside of the pipe, and also the temperature differences all along the pipe requires the use of some average temperature value in order to examine the problem. This average temperature difference is termed as the log mean temperature difference (LMTD).

This is the temperature difference at one end of the heat exchanger minus the temperature difference at another end of the heat exchanger, divided by natural logarithm of the ratio of such two temperature differences. The above definition for LMTD includes two significant suppositions:

(A) The fluid specific heats do not differ significantly with temperature, and (B) the convection heat transfer coefficients are associatively constant during the heat exchanger.