Bernoulli's Equation

Bernoulli's equation is an exceptional case of the general energy equation which is probably the most broadly-used tool for resolving fluid flow troubles. It gives a simple way to associate the velocity head, elevation head, and pressure head of a fluid. It is possible to alter Bernoulli's equation in a way that accounts for head losses and pump work.

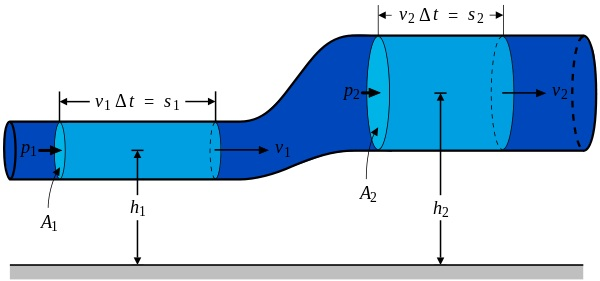
In fluid dynamics, Bernoulli's principle defines that for an inviscid flow, a rise in the speed of the fluid takes place concurrently with reduce in pressure or a reduce in the fluid's potential energy. The Bernoulli's principle is named subsequent to the Swiss scientist Daniel Bernoulli who published his principle in his book Hydrodynamica in the year 1738.

Bernoulli's principle can be applied to different kinds of fluid flow, resultant in what is loosely symbolized as Bernoulli's equation. In fact, there are various forms of the Bernoulli equation for dissimilar types of flow. An easy form of Bernoulli's principle is valid for incompressible flows (example, most liquid flows) and also for compressible flows (example, gases) moving at low Mach numbers. More advanced forms might in some situations be exerted to compressible flows at higher Mach numbers.