Stress-Strain Relationship:

All materials do not behave as mild steel. The stress-strain curves of some materials are giving in Figure. Irrespective of the variety of shapes seen in these curves, one could identify in each of them a segment while the curve might be considered linear. That limit is taken as the elastic limit for the material.

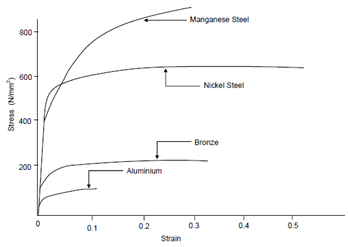
Figure: Stress-Strain Relationship for a Few Materials

The overall behaviour of the material and its full stress-strain relationship is elaborates here only in order to caution the designer to keep the stress level well within the elastic limit. Therefore, for practical reasons the stress-strain relationship is taken as linear and during the rest of this course you will not be dealing along with nonlinearity of material behaviour. Therefore, for a designer, stress is always proportional to the strain and the proportionality constant is described as Elastic Modulus.

Therefore,      Stress, σ = Elastic Modulus (E) × Strain (ε)

or        σ = E . ε                                                                                              . . . (1)

From Eq. (1), we get

E = σ/ε                                                                                                           . . . (2)

Eq. (2) implies that the Elastic Modulus of a material might be computed through measuring the slope of the stress-strain curve (inside the elastic limit). The fact in which Eq. (1) holds good within elastic limit which has already been taught to you as

Hooke's Law that we might restate as follows:

Within elastic limit the strain generates in a solid is always proportional to the stress applied.