Gini Coefficient:

The Gini coefficient (also called the Gini ratio) gives a summary figure for Lorenz curve.  If we  consider the  lower  traingle  (ABD)  in  Fig. 1, the Gini coefficient is given by the following ratio:  

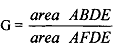
The  Gini  coefficient  was developed to measure  the degree  of  concentration (inequality)  of a variable in a distribution of its elements. The Gini coefficient  ranges between 0 and  1. It assumes a value of zero where all individuals are equal and there is perfect equality in society. On  the other hand, it takes the theoretical maximum of 1 where  in an infinite population  the  income level of every individual except one is zero. The concept of Gini coefficient provides relatively more precise estimates of inequality of incomes in a unit of population.

Gini coefficient is used  to measure income distribution across states, countries and rural and urban areas. If the Gini coefficient  is rising along with  increase in GDP,  it denotes that income inequality  is  increasing.  Gini  coefficient  also  denotes the changes in income levels over a period of time thus indicating income trends as they emerge over a time frame. The measurement based on Gini coefficient suffers due to variations in sample size, size of countries and  non  monetary benefits received  by some sets of population which cannot be easily quantified.