Example:

Find the mean of 67, 88, 91, 83, 79, 81, 69, & 74.

Solution:

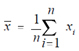
The sum of the scores is 632 and n = 8, therefore

x¯ = 632/8

x¯ = 79

In several cases including statistical analysis, literally hundreds/thousands of data points are involved. In  such  huge  groups  of  data  the  frequency  distribution  can  be  plotted  and  the calculation of the mean can be simplified through multiplying each data point through its frequency distribution, rather than through summing each value. This is especially true while the number of discrete values is little, but the number of data points is large.

Thus, in cases where there is a recurring number of data points, such as taking the mean of a set of temperature readings, it is simpler to multiply each reading through its frequency of occurrence (frequency of distribution), then adding each of the multiple terms to find out the mean.  This is one application using the frequency distribution values of a given set of data.