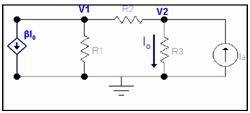
Q:       Determine the value current I₀ by using matrices.

Solution:

            By applying KCL at node 1

                                    βI₀ + V₁/R₁ + (V₁ - V₂)/R₂ =0 ................(i)

            By applying KCL at node 2

                                    (V₂ - V₁)/R₂ +I₀ -I_a =0 ..........................(ii)

                        Here

                                                I_o =V₂/R₃  ....................(1)       

            By simplifying these equations for node 1 & 2 put the value of equation 1 in (i)                 and (ii) we get

                                       β V₂/R₃ + V₁/R₁ + V₁/R₂ - V₂/R₂ = 0

                                    (1/R₁  +1/R₂) V₁ - (1/R₂ - β /R₃) V₂ = 0

            At node 2

                                                -(1/R₂) V₁ + (1/R₂ +1/R₃ )V₂ =Ia

            Or in form of matrix

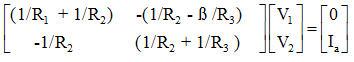
            Now let's find the node voltage for the below given parameters

                                    β =2,   R₂ =6k,   R₁=12k,   R₃=3k,   I_a =2mA

            By using these equations for the network yields we can say

                                              (1/4k) V₁ +(1/2k) V₂ = 0

                                    (1/2k) V₂ - (1/6k) V₁ =2 m A

            Or in the matrix form

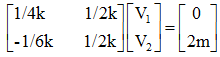
The circuit equations may be solved utilizing matrix analysis. The common form of matrix equation is like

                                                A X = Y or GV=I we have to determine X or V

            In this V or X =    , A or G = and Y or I=

            The answer of the matrix equation is

                                                X = A^-1 Y OR V = G^-1 I --------- (2)

            To determine or G^-1 or A^-1

            We know that G^-1 = Adj(G) / |G| or A^-1 = Adj(A) / |A| 

                        Adjoint of the coefficient matrix A will be

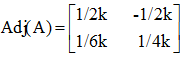
            And the determinant is

                                             | A | = - (1/6k) (-1/2k) +(1/4k) (1/2k) = 5/24k²

                                                A-¹ = Adj(A) / |A| 

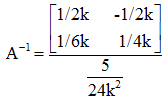
                                    Put A^-1 in equation 2 we get  

Therefore             

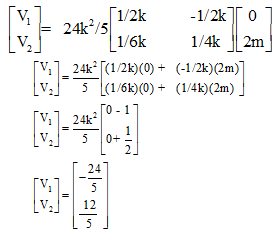
Therefore

                                     V₁  = -24/5volt

                                      V₂ =12/5 volt

                        So the value of  I_o

                                                 I₀ = V2/R₃

                                                      =(12/5)/3k    =4/5k

                                                      = 4/5mA

                                                   I₀= 0.8mA