Multiplication of a Matrix by a Matrix:

For multiply two matrices, the first matrix must have the similar number of rows (m) as the second matrix has columns (n).  Instead, m of the first matrix must equal n of the second matrix. For instance, a 2 x 1 matrix can be multiplied by a 1 x 2 matrix,

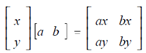
or a 2 x 2 matrix could be multiplied through a 2 x 2.  If an m x n matrix is multiplied by an n x p matrix, after that the output matrix is an m x p matrix.  For instance, if a 2 x 1 and a 1 x 2 are multiplied, the output will be a 2 x 2.  If a 2 x 2 and a 2 x 2 are multiplied, the output will be a 2 x 2.

For multiply two matrices, the subsequent pattern is used:

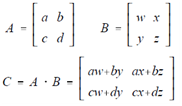
In general terms, a matrix C which is a product of two matrices, A and B, will have elements given by the following.

c_ij  = a_i1b_1j  + a_j2b_2j  + + + . . . + a_inb_nj

where

i = ith row

j = jth column