Q:      Compute the value of current I_3, I₂ & I₁ from Cramer's rule.

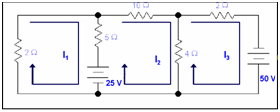
Solution:          We have to use Cramer's rule to solve this example

                                    By using KVL equation at path 1       

                                                            2I₁ + 5( I₁ - I₂)   = -25

                                                            2I₁ +5I₁ - 5I₂      =-25

                                                                  7I₁ - 5I₂        = -25  ----------------- (i)

                                    By applying KVL equation at path 2

                                                10I₂ + + 5(I₂ - I₁) + 4(I₂ - I₃)  = 25

                                                10I₂ + 4I₂ - 4I₃- 5I₁ + 5I₂ = 25

                                                                  -5I₁ + 19I₂ - 4I₃ = 25 ---------------- (ii)

                                    By applying KVL equation at loop 3

                                                            4(I₃ - I₂) + 2I₃ = 50

                                                                     2I₃ + 4I₃ - 4I₂ = 50

                                                                              -4I₂ + 6I₃ = 50 --------------- (iii)

            Write equation (i), (ii) and (iii) In matrix form

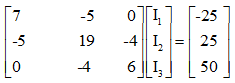
                        Now, the determinant of the coefficient matrix will be

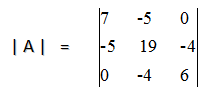
            By apply Cramer's rule

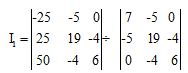
                                                            I₁ = (-700) / 536

                                                             I₁= -1.31 A

            By apply Cramer's rule

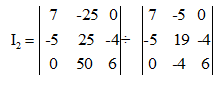
                                                            I₂ = 1700÷536

                                                            I₂ = 3.17A

            By applying Cramer's rule

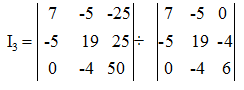
                                                            I₃ = 5600/536

                                                               I₃ = 10.45 A