Number System:
Natural Number:
The numbers 1, 2, 3, 4.... Are known as natural numbers, their set is shown by N. Hence N = {1, 2, 3, 4, 5....}
Whole Number:
The numbers 0, 1, 2, 3, 4...... Are known as whole numbers, their set is presented by W. therefore W = {0, 1, 2, 3, 4....}
Integers:
The numbers. ...- 3, -2, -1, 0, 1, 2, 3....are known as integers and their set is shown by I & Z
Set of positive integers shown by I+ and consists of {1, 2, 3...}, also called as set of natural numbers.
Set of negative integers shown by I- and consists of {...- 3, - 2, - 1}
Set of non-negative integers is {0,1,2, 3...} also called as set of whole numbers
Set of non-positive integers is {...- 3, - 2, - 1, 0}
Rational Numbers:
All numbers of the type p/q where p and q are integer and q ≠ 0, are known as rational.
Thus
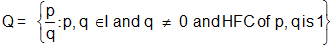
it can be noticed that every integer is a rational number it may be defines as p/1. As like are 1/3, - 4/9 and 57 The rational numbers are similarly the real numbers with decimal expansions that are either Terminating (finishing in an infinite string of zeros), for example 3/4 = .75000... = .75. Non-ermating Repeating (finishing with a block of digits that repeats over and over).
For example 23/11 = 2.090909... = 2.09. The bar defines the block of repeating digits.
Irrational Numbers:
Real numbers that are not rational are known as irrational numbers. They are exactly the real numbers with decimal expansions that are non-repeating non-terminating. Their set is shown by Qc (i.e. complementary set of Q) As like are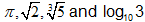
Real Numbers:
|
The hole set of irrational and rational numbers is the set of real numbers and is shown by R. Therefore R = Q ∪ Qc. The real numbers can also be define in terms of position of a point on the real line (is the number line wherein the position of a point belongs to the origin (i.e. 0) shows a unique real number and vice versa). All the numbers given so far follow the order property i.e. if there are two numbers a & b then either a < b or a = b or a > b
|
|
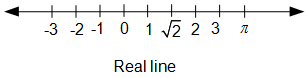
Complex Numbers:
A number of the form x + iy, where x and y are real and natural numbers and i=√-1, is known as a complex number. It is generally shown by z. i.e. z = x + iy, x is known as the real part and y the imaginary part of z. C shows the set of complex number.
Note: The system of complex numbers adds the system of real numbers, i.e. R ⊂ C.
Problem: If a and b are two different rational numbers such that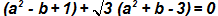 
, find a and b.
Solution: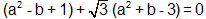 
{Rational} {Irrational}
=> a2 - b + 1 = 0 and a2 + b - 3 = 0
=> a = ±1 and b = 2