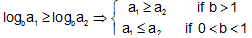Logarithmic function:

The logarithm of a provided number b to the base 'a' is the exponent showing the power to which the base 'a' have to be raised to get the number b. This number is defined as log _a b. Therefore log _a b = x <=> a^x = b, a > 0, a≥1 and b>0. From the basic definition of the logarithm of the number b to the base 'a', we have an identity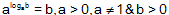 

That is called as Fundamental Logarithmic Identity.

Properties of logarithmic function

The function log_ab is significant for b >0 and for either 0 < a < 1 or a > 1.

Let a > 1, then 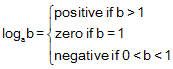 and

      If 0 < a < 1, then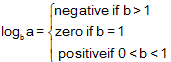 

log _a(mn) = log _a m + log _a n

 , c > 0 and c ¹ 1.

log _{a logcb/ logca} = log _a m - log _a n

log _a mⁿ = n log _a m

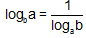 provided both a and b are non-unity.

log_a1 = 0

log_aa = 1