L'Hopital's Rule
A rule is useful in evaluating indeterminate forms: if both functions ƒ(x) and g(x) and all their derivatives up to order (n- 1) vanish at x=a, but the nth derivatives do not vanish or become infinite at x=a, then ƒ(n)denoting the nth derivative.
In calculus, l'Hôpital's rule uses derivatives to assist evaluate limits involving the indeterminate forms. Application of the rule converts an indeterminate form to a determinate form, allowing easy evaluation of limit.
Assume that we want to find the value of
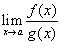 ,
,
when f (a) = g (a) = 0. One method is to make use of L'Hopital's Rule, which says: if f (x) and g (x) are differentiable functions and f (a) = g (a) = 0, then
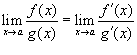 ,
,
if limit on the right exists. Or we can say that, we can find the original limit by finding the limit of ratio of the derivatives of the denominator and numerator functions.
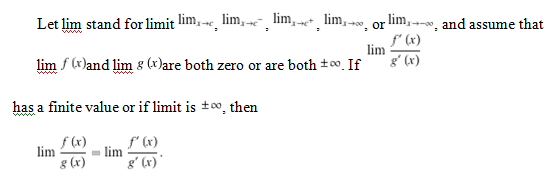
|
Procedure of differential calculus for evaluating indeterminate forms like 0/0 and ∞/∞ when they result from attempting to find a limit. It states that when limit of f(x)/g(x) is indeterminate, under some conditions it can be obtained by evaluating the limit of the quotient of the derivatives of f and g (that is, f′(x)/g′(x)). If the result is indeterminate, the procedure can be repeated again. It is named after the French mathematician Guillaume de L'Hôpital.
|
www.expertsmind.com - L’Hopital’s Rule Assignment Help, L’Hopital’s Rule Homework Help, L’Hopital’s Rule Assignment Tutors, L’Hopital’s Rule Solutions, L’Hopital’s Rule Answers, Math Assignment Tutors