Inequalities:

If p, q and r are real numbers, then

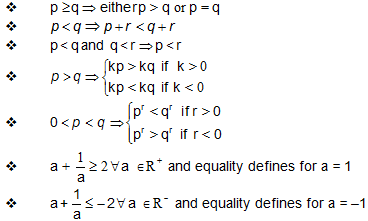
In equation having Exponential Expression:

• If k > 0, then k^x > 0 for all real x.
• If k > 1, then k^x > 1, when x > 0
• If 0 < k < 1, then k^x < 1, when x > 0 and k^x > 1, when x < 0.

Problem: Solve the inequality (x)^{x - 2} > 1.

Solution:             Case I:     When x > 1, x^{x - 2} > 1

                                                Þ x - 2 > 0 => x > 2

                                                So, solution set is x ∈ (2, ∞).

                              Case II:    When 0 < x < 1, x^{x - 2} > 1

                                                Þ x - 2 < 0 => x < 2.

                                                So, solution in that case is x ∈ (0, 1)

                                                So, solution set is x ∈ (0, 1) ∪ (2, ∞).