Absolute value:

Consider x ∈ R.

Then the magnitude of x is known as it's absolute value and in general, shown by |x| and is described as .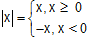

Since the symbol √a always shows the nonnegative square root of a, an alternate definition of |x| is |x| = √x² .

Geometrically, |x| shows the distance of number 'x' from the origin, calculated along the number line. Same as |x - a| shows the distance between a and x. There is other term to describe |x| as |x| = max {x, - x}.

Fundamental Properties:

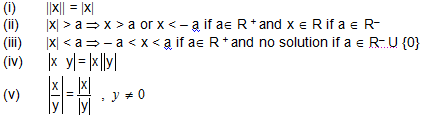
(vi)       |x+y|≤|x|+|y| Here the equality sign defines if x and y either both are non-positive or non-negative in another words x.y≥0.

(vii)      |x+y|≥|x|-|y| Here the equality sign defines if x and y either both are non-positive or non-negative in another words x.y≤0.

The last two properties may be put in one compressed form namely,