How Acceleration Is Determined:

Acceleration magnitude is expressed in meters per second per second, also known as meters per second squared (m/s²). This may seem esoteric at first. What is a second squared? Think of it in terms of a concrete illustration. Assume that you have a car which can go from 0 to 60 miles per hour (0.00 to 60.0 mi/h) in 5 seconds (5.00 s). A speed of 60.0 mi/h is approximately equal to 26.8 m/s. Assume that the acceleration rate is constant from the instant you first hit the gas pedal until you have reached a speed of 26.8 m/s on a level straightaway. Then you can compute the acceleration magnitude:

a = (26.8 m/s)/(5 s) = 5.36 m/s²

Obviously the instantaneous acceleration will not be constant in a real-life test of a car's get-up-and-go power. Though, the average acceleration magnitude will still be 5.36 m/s² -a speed increase of 5 meters per second with each passing second-supposing that the vehicle's speed goes from 0.00 to 60.0 mi/h in 5.00 s.

Instantaneous acceleration magnitude can be measured in terms of the force it applies on a known mass. This can be determined according to the quantity of distortion in an elastic object like a spring. The "force meter" which is as shown in figure below can be adapted to make an "acceleration meter," technically termed as an accelerometer, for measuring acceleration magnitude. A fixed, known mass is located in the device, and the deflection scale is calibrated in a laboratory environment. For the accelerometer to work, the direction of the acceleration vector should be in line with the spring axis, and the acceleration vector should point outward from the fixed anchor toward the mass. This will generate a force on the mass directly against the spring. A functional diagram of the fundamental arrangement is as shown in the next figure below.

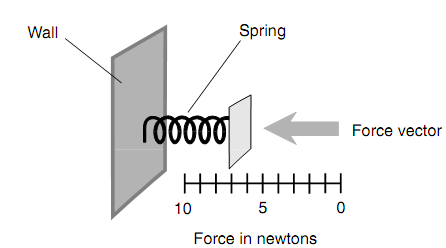
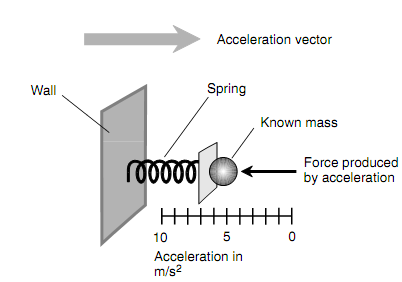
Figure: An accelerometer. It measures the magnitude only and should be oriented properly to give an accurate reading.

A general spring scale can be used to measure acceleration indirectly. Whenever you stand on the scale, you compress a spring or balance a set of masses on a lever. It measures the downward force which the mass of your body exerts as an outcome of a phenomenon known as the acceleration of gravity. The effect of gravitation on a mass is similar as that of an upward acceleration of around 9.8 m/s². Mass, force, and acceleration are intimately associated.

Assume that an object begins from a dead stop and accelerates at an average magnitude of a_avg in a straight line for a time period t. Assume, after this length of time, that the magnitude of the displacement from the beginning point is q. Then this formula may apply:

q = a_avg t²/2

In this illustration, assume that the acceleration magnitude is constant; say it a. Let the instantaneous speed be called v_inst at time t. Then the instantaneous speed is associated to the acceleration magnitude as follows:

v_inst= at

PROBLEM:

Assume that two objects, symbolized by curves A and B as shown in figure below, accelerate all along straight-line paths. What is the instantaneous acceleration a_inst at t = 4 seconds for object A?

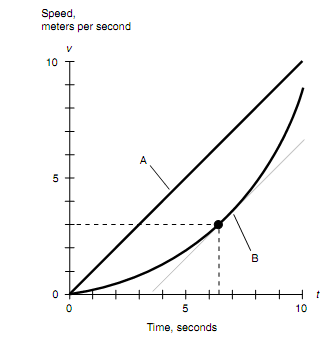
SOLUTION:

The acceleration represented by curve A is constant as the speed increases at a constant rate with time. (This is why the graph is a straight line.) The number of meters per second squared does not change throughout the time duration shown. In 10 seconds, the object accelerates from 0 to 10 m/s; this is a rate of speed increase of 1 meter per second per second (1 m/s²). And hence, the acceleration at t = 4 s is a_inst = 1 m/s².