Product of inertia of rigid bodies:

In case of thin plane plates where the mass of the shape is proportional to the area, the term mass moment of inertia may be replaced by the term area moment of inertia.

The values of mass moment of inertia and product of inertia of rigid bodies depend upon the location of x, y, z axes.

Considering Figure wherein the origin of our selected frame of reference coincides with the mass centre C of the body, then these axes are referred as centroidal axes and are mentioned by x₀ , y₀ , z₀ . Let a particle of mass dm situated at k from C, and its coordinates be x₀ , y₀ , z₀ , then we have :

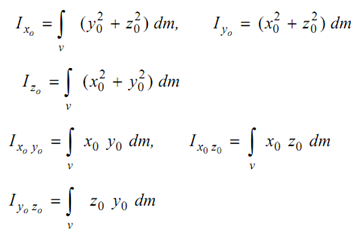
Corresponding inertia terms about any axes x, y, z which are parallel to the centroidal axes may be calculated as below.

As illustrated in Figure, the coordinates of point k, w.r.t. to x, y, z axes may be written as

x = x₀  + x_c , y = y₀  + y_c , z = z₀ + z_c

where,  x_c , y_c  and z_c are the coordinates of the mass centre C with respect to any other x, y, z axes.

Now we may write moment of inertia about x axis as :

I _x  = ∫ ( y ²  + z ² ) dm = ∫ ( y₀  + y_c )²  dm + ∫ ( z₀  + z_c )²  dm

= ∫ (y₀ )² dm + ∫ (z₀ )²  dm + ∫(y_c )²  dm + ∫ z_c²  dm

∫y₀  y_c  dm +  2 ∫ z₀  z_c  dm

But we know that,

∫  y₀ y_c  dm = y_c  ∫ y₀  dm = 0

and,

∫  z₀ z_c  dm = z_c  ∫ z₀  dm = 0

And from Eq. (7.4)

∫ (y₀) ² dm + ∫ (z₀ )²  dm =  ∫  (y _o)² + (z _o )²) dm = Ix₀

 ∫ (y _c )²                        dm = m(y_c)² ,   and ∫( z _c )²  dm = m (z _c )²

Therefore, we have

I x = I x₀    + m ((y_c )²+ (z_c )²)

Similarly, it can be shown that

I y = I y₀    + m ( (x_c)² + (z_c)²)

I z = I z₀    + m ((x_c )²+ (y_c)²)

I xy = I x ₀ y₀ + mx_c  y_c ,

I yz = I y₀  z ₀ + my_c z_c                     etc

 The above results are called as parallel axes theorem. These are very much useful in determining of inertia properties of rigid bodies.