Mass moment of inertia of a body:

The mass moment of inertia of a body is generally calculated about three mutually perpendicular axes x, y, z as illustrated in Figure.

Consider again a particular mass dm at k whose coordinates are x, y, z. Its perpendicular

distance from the x axis shall be 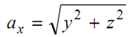so that the moment of inertia of the

body about this axis shall be

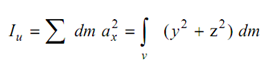
Similarly, we may write

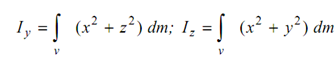
The corresponding radii of gyrations are given by

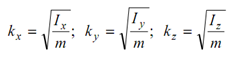
Additionally to moment of inertia of the body, an additional property known as product of inertia is also required. Referring to Figure, product of inertia I_xy of the body about the relevant axis may be written as

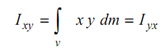
Likewise

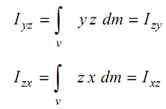
The polar moment of inertia of the body around the point O (here the origin of axes) is defined as : 

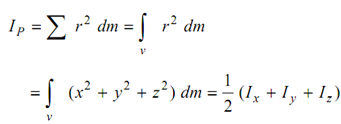--------- (3)

 The moment of inertia involves quadratic terms, therefore, this is always positive. While product of inertia can be positive, negative or zero.

In case of thin plane plates where the mass of the shape is proportional to the area, the term mass moment of inertia may be replaced by the term area moment of inertia.

The values of mass moment of inertia and product of inertia of rigid bodies depend upon the location of x, y, z axes.